Année : 2023 2022 2021 2020 2019 2018 2017 2016 2015 2014 2013 2012 2021 2020 2019 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2004 2003 2002 2001 2000 1999 1998 1997 1996

• Année :
• 2023
• 2022
• 2021
• 2020
• 2019
• 2018
• 2017
• 2016
• 2015
• 2014
• 2013
• 2012
• 2011
• 2010
• 2009
• 2008
• 2007
• 2006
• 2005
• 2004
• 2003
• 2002
• 2001
• 2000
• 1999
• 1998
• 1997
• 1996

Semaine 9

• Problème (publié le 29 octobre)

  Dans un triangle $\Delta ABC$ nous notons les côtés de la façon suivante: $AB=c, AC=b, BC=a$. Soit $D$ le point sur le côté $BC$ tel que $AD$ est la bissectrice de l'angle $\angle BAC$. Soit $E$ la réflexion $D$ par rapport au point milieu $M$ du segment $BC$ et soit $F$ le point sur le segment $BC$, tel que $\angle BAF =\angle EAC$. Montrer que $$ \frac{BF}{FC}=\frac{c^3}{b^3} \,. $$

• Solution (publié le 5 novembre)

  Problème 4 de la $30^e$ Olympiade Mathématique Espagnole, Première Manche, 1993, paru dans Crux Mathematicorum [1998: 69]. Nous présentons la solution de Toshio Seimiya, telle que présentée dans [1999: 201-203].

  Note: Une solution vidéo (en anglais) est aussi disponible.

  Soit $T$ le point sur $AF$ tel que $BT \parallel AC$ et soit $S$ le point sur $AE$ tel que $CS \parallel AB$.

  

  Nous avons \begin{align} \angle ABT&+\angle BAC=180^\circ \cr \angle ACS&+\angle BAC=180^\circ \,. \end{align} Ainsi, $\angle ABT = \angle ACS$ et $\angle BAT =\angle CAS$, ce qui montre que $\Delta BAT \sim \Delta CAS$. Ceci nous donne que \begin{equation}\tag{1} \frac{AT}{AS}=\frac{BT}{CS}=\frac{c}{b} \,. \end{equation} Comme $BT \parallel AC$ nous avons que $\Delta BFT \sim \Delta CFA$ et, par conséquent, \begin{equation}\tag{2} \frac{BF}{FC}=\frac{FT}{AF}=\frac{BT}{b} \,. \end{equation}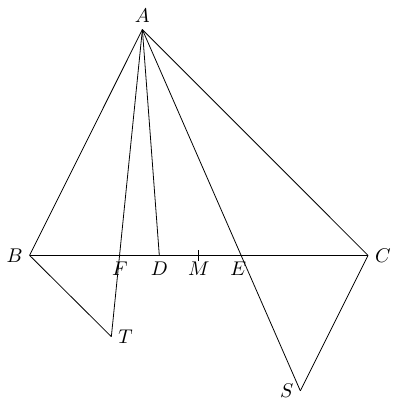

  De façon semblable, $CS \parallel AB$ implique que $\Delta ABE \sim \Delta CSE$, ce qui implique que \begin{equation}\tag{3} \frac{BE}{CE}=\frac{AE}{SE}=\frac{c}{CS} \,. \end{equation}

  Comme $E$ est la réflexion de $D$ par rapport à $M$ nous avons $EC=BD$ et $BE=CD$. Ainsi, $$ \frac{BE}{EC}=\frac{DC}{DB} \,. $$

  Finalement, comme $AD$ est la bissectrice de l'angle $\angle BAC$, le théorème de la bissectrice (Bissector Theorem) nous donne que \begin{equation}\tag{4} \frac{DC}{DB}=\frac{b}{c} \,. \end{equation}

  En combinant l'équation (3) et l'équation (4), nous obtenons $$ \frac{c}{CS}=\frac{b}{c} \Rightarrow CS=\frac{c^2}{b} \,. $$ Alors, par l'équation (1), nous obtenons $$ BT=\frac{c^3}{b^2} \,. $$

  Finalement, l'équation (2) nous donne $$ \frac{BF}{FC}=\frac{BT}{b}=\frac{c^3}{b^3} \,. $$ ∎

Semaine 8

• Problème (publié le 22 octobre)

  Soit $a_1,a_2,..., a_n, b_1, b_2,...b_n$, $2n$ nombres réels tels que $a_1,a_2,..., a_n$ sont distincts. S'il existe un nombre réel $\alpha$ tel que pour tout $1 \leq j \leq n$ nous avons $$ (a_j+b_1)\cdot(a_j+b_2) \cdot \ldots \cdot (a_j+b_n) =\alpha \,, $$ montrer qu'il existe également un nombre $\beta$ tel que pour tout $1 \leq k\leq n$ nous avons $$ (a_1+b_k)\cdot(a_2+b_k) \cdot \ldots \cdot (a_n+b_k) =\beta \,. $$

• Solution (publié le 29 octobre)

  Problème 2 du Deuxième Questionnaire de la Sixième Olympiade Mathematique Irlandaise, paru dans Crux Mathematicorum [1995: 152]. Nous présentons la solution de Michael Selby, telle que présentée dans [1997: 141-142].

  Note: Une solution vidéo (en anglais) est aussi disponible.

  On pose $$ P(X)=(X+b_1)\cdot(X+b_2)\cdot \dots \cdot (X+b_n) -\alpha\,. $$ De cette façon, $P(a_1)=P(a_2)=...=P(a_n)=0$. Ainsi, comme $a_1,a_2,...,a_n$ sont distincts, par le théorème de Factorisation (Factor Theorem), nous avons $$ P(X)=(X-a_1)\cdot(X-a_2) \cdot \dots \cdot (X-a_n) \,. $$ Ce qui donne \begin{equation}\tag{1} (X+b_1)\cdot(X+b_2)\cdot \dots \cdot (X+b_n) -\alpha=(X-a_1)\cdot(X-a_2) \cdot \dots \cdot (X-a_n) \,. \end{equation} Maintenant, pour tout $1 \leq k \leq n$, substituons $X=-b_k$ dans l'équation (1), ce qui donne $$ 0-\alpha=(-1)^{n} (a_1+b_k)\cdot(a_2+b_k) \cdot \dots \cdot (a_n+b_k) \,. $$ Ainsi, pour tout $1 \leq k \leq n$ nous avons $$ (a_1+b_k)\cdot(a_2+b_k) \cdot \dots \cdot (a_n+b_k) = (-1)^{n+1} \alpha \,. $$ Le nombre $\beta=(-1)^{n+1} \alpha$ respecte la contrainte et c'est ce que nous recherchions.

Semaine 7

• Problème (publié le 15 octobre)

  Un triangle équilatéral de côté $6$ est divisé en $36$ petits triangles équilatéraux de côté $1$. Nous construisons des morceaux de type $A$, formés de deux triangles équilatéraux de côté $1$ et des morceaux de type $B$, formés de trois triangles équilatéraux de côté 1. Ceux-ci sont illustrés sur la figure ci-dessous. On recouvre le grand triangle avec $m$ morceaux de type $A$ et $n$ morceaux de type $B$, sans superposition et sans espace vide. Déterminer toutes les valeurs possibles de $m$.

  

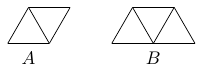
• Solution (publié le 22 octobre)

  Problème 2 de l'Olimpiada Nacional Escolar de Matematica 2009, Niveau 2, paru dans Crux Mathematicorum [2010: 373]. Nous présentons la solution de Chip Curtis, telle que présentée dans [2011: 425-426], modifiée par l'éditeur.

  Note: Une solution vidéo (en anglais) est aussi disponible.

  Comme chaque morceau de type $A$ couvre deux triangles et que chaque morceau de type $B$ en couvre trois, nous avons que $$ 2m+ 3n = 36 \,. $$ Ce qui nous donne les valeurs de $m$ suivantes $$ m \in \{ 0, 3, 6, 9, 12, 15, 18 \} \,. $$ Nous montrons que les valeurs de $m = 0, 3, 6, 9$ sont possibles et que les valeurs de $m = 12, 15, 18$ sont impossibles.

  Les figures suivantes montrent que les valeurs de $m=0,3,6,9$ sont possibles.

  

  

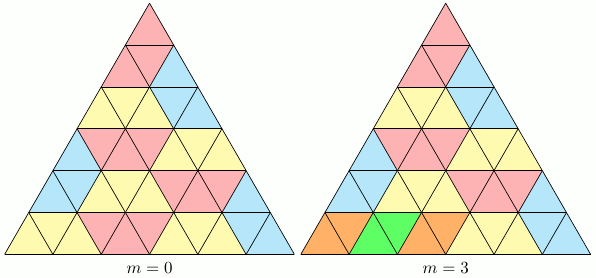
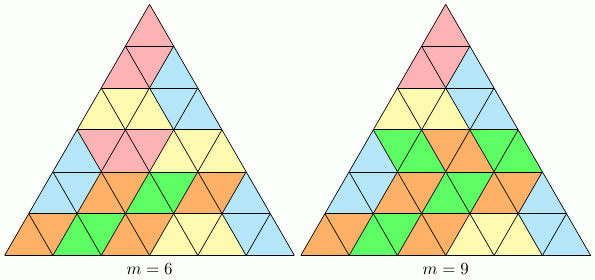
  Pour montrer que les valeurs de $m = 12, 15, 18$ sont impossibles, nous colorons les petits triangles de la figure de deux couleurs différentes en alternance, tel qu'illustré ci-dessous.

  

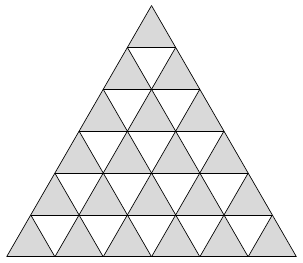
  Remarquons que les morceaux de type $A$ couvrent exactement un triangle blanc et un triangle gris. Ceux de type $B$ couvrent soit deux triangles blancs et un gris, soit deux triangles gris et un blanc.

  Comme il y a $6$ triangles gris de plus que de triangles blancs, nous devons utiliser au moins $6$ morceaux de type $B$. Ainsi, nous avons que $n \geq 6$. Donc $$ m=\frac{36-3n}{2} \leq \frac{36-18}{2} =9 \,. $$

  Ce qui montre que les valeurs de $m = 12, 15, 18$ sont impossibles et que $$ m \in \{ 0, 3, 6, 9 \} \,. $$

Semaine 6

• Problème (publié le 8 octobre)

  Trouver toutes les fonctions $f: \mathbb{R} \rightarrow \mathbb{R}$ respectant la propriété suivante pour tout $x,y \in \mathbb{R}$: \begin{equation}\tag{1} f(xf(x)+f(y)) = (f(x))^2 + y. \end{equation}

• Solution (publié le 15 octobre)
  Note: Une solution vidéo (en anglais) est aussi disponible.

  Problème 1 de la 17e Olympiade Mathématique des Balkans, paru dans Crux Mathematicorum [2004: 84]. Nous présentons la solution de José Luis Díaz-Barrero, telle que rédigée dans [2005: 523-524].

  Il est facile de voir que la fonction $f(x)=x$ pour tout $x \in \mathbb{R}$ et que la fonction $f(x)=-x$ pour tout $x \in \mathbb{R}$ satisfont l'équation (1). Nous allons montrer que ce sont les seules solutions.

  Posons $a=f(0)$. En fixant $x=0$ dans l'équation (1) nous obtenons \begin{equation}\tag{2} f(f(y))=y+a^2 \,. \end{equation} Prenons $b=f(-a^2)$. Alors $f(b)=f(f(-a^2))=-a^2+a^2=0$.

  En fixant $x=b$ dans l'équation (1) nous obtenons \begin{equation}\tag{3} f(f(y))=y \,. \end{equation} En combinant l'équation (2) et l'équation (3), nous obtenons $a=0$, ce qui implique que $f(0)=0$. En fixant $y=0$ dans (1) nous obtenons \begin{equation}\tag{4} f(xf(x))=\left( f(x) \right)^2 \,. \end{equation}

  Maintenant, prenons $t \in \mathbb R$ un nombre arbitraire. En fixant $x=f(t)$ dans l'équation (4) et en utilisant le fait que, par l'équation (3) nous avons $f(x)=t$ nous obtenons \begin{equation}\tag{5} f(tf(t))=\left( f(f(t)) \right)^2=t^2 \,. \end{equation}

  Ainsi, pour tout $x \in \mathbb R$ nous avons, par l'équation (4) et l'équation (5), que \begin{equation}\tag{6} x^2=f(xf(x))=(f(x))^2 \,. \end{equation}

  Cela nous donne $f(x)=\pm x$ pour tout $x \in \mathbb{R}$. Alors, pour tout $x \in \mathbb{R}$ nous avons seulement $f(x)=x$ ou $f(x)=-x$. Pour compléter la solution, il faut montrer que le signe reste le même pour tout $x$.

  Supposons, afin d'obtenir une contradiction, qu'il existe deux nombres non-nuls $\alpha, \beta$ tels que $f(\alpha)=\alpha$ et $f(\beta)=-\beta$. Alors, en fixant $x=\alpha, y=\beta$ dans (1) nous obtenons $$ f \left(\alpha^2-\beta \right)= \alpha^2+\beta \,, $$ qui implique, par l'équation (6), que $$ \left(\alpha^2-\beta \right)^2=\left(\alpha^2+\beta \right)^2 \,. $$ En développant, nous obtenons $\alpha^2 \beta=0$ ce qui contredit le fait que $\alpha, \beta$ sont tous deux différents de $0$.

  Comme nous avons obtenu une contradiction, notre hypothèse était fausse. Par conséquent, les seules solutions sont la fonction $f(x)=x$ pour tout $x \in \mathbb{R}$ et la fonction $f(x)=-x$ pour tout $x\in \mathbb{R}$.

  Note de l'éditeur: Ce problème est similaire au Problème de la semaine 4 du COMC 2014, voir https://docm.math.ca/2014/potw.html.

Semaine 5

• Problème (publié le 1 octobre)

  Déterminer tous les triplets $(x,y,z)$ constitués d'entiers naturels qui satisfont l'équation $$ \frac{1}{x}+\frac{2}{y}-\frac{3}{z}=1\,. $$

• Solution (publié le 8 octobre)

  Problème 3 de la $26^e$ Olympiade Mathématique Belge, paru dans Crux Mathematicorum [2004: 268]. Nous présentons la solution de Pierre Bornsztein, telle que rédigée dans [2006: 153].

  Note: Une solution vidéo (en anglais) est aussi disponible.

  Soit $(x,y,z)$ une éventuelle solution du problème. Alors $$ yz+2xz=3xy+xyz \,. \tag{1} $$ Supposons que $x \geq 3$ et $y \geq 3$. Nous pouvons donc affirmer que $3(x-1)>2x$ et que $3xy >0$. Ce qui nous permet d'écrire: \begin{align} 3xy+xyz \geq xyz &= yz + (x-1)yz \cr &= yz + 3(x-1)z \cr &> yz + 2xz \,, \end{align} ce qui contredit l'équation (1). Nous obtenons donc $x <3$ ou $y<3$. Ce qui nous permet de procéder par cas:

  • Supposons d'abord que $y \geq 3$. Alors $x=1$ ou $x=2$.

    Si $x=2$, on veut résoudre $$ yz+4z=6y+2yz \Rightarrow yz+6y-4z=0 \Rightarrow (y-4)(z+6)=-24 \,. $$ Or, $y-4 \geq -1$ et $z+6 \geq 7$, donc $y-4=-1$ et $z+6=24$. Cela conduit au triplet suivant: $$ (x,y,z)=(2,3,18) \,. $$ qui est effectivement une solution.

    Si $x=1$, on veut résoudre $$ yz+2z=3y+yz \Rightarrow 3y= 2z $$ ce qui conduit directement à $$ (x,y,z)=(1,2a,3a) \,, $$ où $a \geq 2$ est un entier (car $y \geq 3$).

    Encore une fois, on vérifie facilement qui ces triplets sont bien solutions.

  • Si $y=2$, l'équation (1) devient $$ 2z+2xz=6x+2xz \Rightarrow z=3x \,, $$ ce qui conduit directement à $$ (x,y,z)=(b,2,3b) \,, $$ où $b \geq 1$ est un entier. Notons que l'on récupère le cas où $a=1$ pour les triplets de la section précédente.
  • Si $y=1$ l'équation (1) devient $$ z+2xz=3x+xz\Rightarrow xz-3x+z=0 \Rightarrow (x+1)(z-3)=-3 \,, $$ avec $x+1 \geq 2$. Cela conduit à $x+1=3, z-3=-1$, c'est à dire $$ (x,y,z)=(2,1,2) \,. $$ On vérifie également que le triplet $(2,1,2)$ est une solution.

    Finalement, les solutions sont les triplets de la forme $(1, 2a, 3a), (a, 2, 3a)$ où $a>0$ est un entier, ainsi que les deux triplets suivants: $(2,1,2)$ et $ (2,3,18)$.

Semaine 4

• Problème (publié le 24 septembre)

  Étant donné que $$\left(x+\sqrt{x^2+1}\right)\left(y+\sqrt{y^2+1}\right)=1.$$ Montrer que $x+y = 0$.

• Solution (publié le 1 octobre)

  Problème 2 de la $31^e$ Olympiade Mathématique Espagnole, Premier Tour, paru dans Crux Mathematicorum [1998: 453]. Nous présentons la solution de Mohammed Aassila, telle que présentée dans [2000: 142], modifiée par l'éditeur.

  Note: Une solution vidéo (en anglais) est aussi disponible.

  Posons $z=x+\sqrt{x^2+1}$. Alors, $z>0$ et $$ \frac{1}{z}=\frac{\sqrt{x^2+1}-x}{x^2+1-x^2}=\sqrt{x^2+1}+x-2x=z-2x \,, $$ que l'on peut réécrire comme $$ x=\frac{z^2-1}{2z} \,. $$ De même, \begin{align} z(y+\sqrt{y^2+1})&=1 \qquad \Rightarrow \cr y+\sqrt{y^2+1}&=\frac{1}{z} \qquad \Rightarrow \cr z=\frac{\sqrt{y^2+1}-y}{y^2+1-y^2}&=\sqrt{y^2+1}+y-2y=\frac{1}{z}-2y \Rightarrow \cr y&=\frac{1-z^2}{2z} \,. \end{align} En combinant les deux parties, nous obtenons $$ x+y= \frac{z^2-1}{2z} + \frac{1-z^2}{2z} =0 \,. $$

  ∎

  Notes de l'éditeur: Si vous êtes familiers avec les logarithmes et les fonctions hyperboliques inverses, vous aimerez probablement la solution de Michel Battaille: En prenant les logarithmes et en utilisant le fait que $\sinh^{-1}(x)=\ln\left(x+\sqrt{x^2+1}\right)$ l'équation devient $$ \sinh^{-1}(x)+\sinh^{-1}(y) =0 \,. $$ Comme $\sinh^{-1}(x)$ est une fonction impaire et bijective, nous obtenons $$ \sinh^{-1}(x)=\sinh^{-1}(-y) \Rightarrow x=-y \,. $$

Semaine 3

• Problème (publié le 17 septembre)

  Nous définissons la suite $a_1, a_2 , a_3 , \dots$ de la façon suivante

  $ a_1$	$=a_2=1003$
  $a_{n+1}$	$=a_n-a_{n-1} \qquad$ for all $n \geq 2 \,.$

  Calculer la somme des 2006 premiers termes de la suite.

• Solution (publié le 24 septembre)

  Problème 3 de l'Olympiade mathématique de l'Asociación Venezolana de Competencias Matemáticas, 2006, paru dans Crux Mathematicorum [2009:380]. Nous présentons la solution d'Oliver Geupel, telle que rédigée dans [2011:278].

  Note: Une solution vidéo (en anglais) est aussi disponible.

  Nous avons

  $a_3$	$=a_2-a_1=0 $
  $a_4$	$=a_3-a_2=-1003 $
  $a_5$	$=a_4-a_3=-1003 $
  $a_6$	$=a_5-a_4=0 $
  $a_7$	$=a_6-a_5=1003=a_1 $
  $a_8$	$=a_7-a_6=1003=a_2 $

  Il suit de ceci que la suite est cyclique de période $6$. De plus, la some de 6 termes consécutifs est 0.

  Ainsi, comme $2004=6 \cdot 334$ nous obtenons

  $\displaystyle\sum_{k=1}^{2006}a_k $	$\displaystyle = a_1+a_2 + \sum_{j=0}^{333} \left( a_{6j+3}+a_{6j+4}+a_{6j+5}+a_{6j+6}+a_{6j+7}+a_{6j+8} \right)$
  	$=a_1+a_2$
  	$=2006 \,.$ ∎

Semaine 2

• Problème (publié le 10 septembre)

  Combien de sous-ensembles de trois éléments peut-on former à partir de l'ensemble $\{ 1 , 2 , 3, \dots , 20 \}$ de sorte que $4$ divise le produit des trois nombres du sous-ensemble?

• Solution (publié le 17 septembre)

  Problem 1 du Concours de Mathématique Islandais 2004-05, paru dans Crux Mathematicorum [2008:285]. Nous présentons la solution de John G. McLoughlin telle que rédigée dans [2009:386].

  Note: Une solution vidéo (en anglais) est aussi disponible.

  Il y a $\binom{20}{3}=1140$ sous-ensembles de trois éléments au total. Nous comptons combien ne répondent pas aux critères du problème.

  Premièrement, remarquons que les seuls sous-ensembles qui ne répondent pas aux critères sont les suivants:

  • tous les éléments sont impairs.
  • deux éléments sont impairs et le troisième est pair, mais n'est pas un multiple de $4$.

  Dans le premier cas, il y a $\binom{10}{3}=120$ sous-ensembles ne comportant que des nombres impairs.

  Dans le second cas, il y a $\binom{10}{2}\binom{5}{1}=225$ comportant deux nombres impairs et un nombre pair qui n'est pas un multiple de $4$.

  Ainsi, il y a au total $$ 1140-120-225=795 $$ tels sous-ensembles. ∎

Semaine 1

• Problème (publié le 3 septembre)

  Cette semaine, nous donnons deux problèmes plus accessibles.

  Problème A
  Soit $x$ un entier de la forme $$ x=\underbrace{111\dots11}_{n \mbox{ fois }} $$ Montrer que si $x$ est premier, alors $n$ est aussi premier.

  Problème B
  Étant donné un rectangle de côtés $a$ et $b$, tel qu $a>b$, on effectue un pli le long de la diagonale. Déterminer l'aire de la région triangulaire délimitée par la superposition des deux moitiés du rectangle (la région ombragée sur l'image).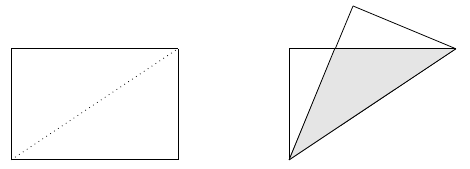

  

• Solution (publié le 10 septembre)

  Problème A

  Problème 7 de l'Olympiade Mathématique Chilienne 1994-95, paru dans Crux Mathematicorum [2001: 170]. Nous présentons la solution de Christopher J. Bradley telle que rédigée dans [2003: 294].

  Note: Une solution vidéo (en anglais) est aussi disponible.

  Remarquons que $$ 9x=\underbrace{999\dots 99}_{n \mbox{ fois }}=10^n-1 \,. $$ Alors, $$ x=\frac{10^n-1}{9} \,. $$ Pour obtenir une contradiction, nous supposons que $n$ est composé, $n = n_1n_2$ avec $n_1, n_2>1$. Ainsi $$ x=\frac{10^n-1}{9}=\frac{10^{n_1}-1}{9} \left(1+10^{n_1}+10^{2n_1}+\dots+10^{n_1(n_2-1)} \right)\,. $$ Comme $\frac{10^{n_1}-1}{9}$ est un entier plus grand que $1$ et $1+10^{n_1}+10^{2n_1}+\dots+10^{n_1(n_2-1)}>1$ nous obtenons que $x$ est composé, une contradiction.

  Comme nous avons obtenu une contradiction, notre hypothèse que $n$ est composé est fausse.

  Alors, $n$ n'est pas composé et $n\neq 1$ (car $x=1$ n'est pas premier), ce qui prouve que $n$ est premier. ∎

  Note de l'éditeur: Les premiers de cette forme sont parfois appelés « premiers répunits », une francisation du terme anglais repunit pour répétition de l'unité. Jusqu'à présent, 5 premiers répunits ont été découverts, à savoir des valeurs de $x$ pour $n \in \{ 2, 19, 23, 317, 1031 \}$. Les valeurs de $x$ pour $n \in \{ 49081, 86453, 109297, 270343\}$ sont également soupçonnées d'être des premiers.

  Problème B

  Problème 1 du XV Gara Nazionale di Matematica 1999, paru dans Crux Mathematicorum [2002:481] . Nous présentons la solution de Bob Serkey telle que rédigée dans [2005:37].

  Note: Une solution vidéo (en anglais) est aussi disponible.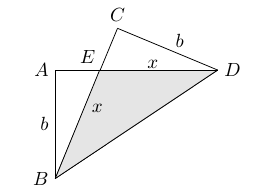

  

  Soit $E$ l'intersection de $BC$ et $AD$, et posons $x=BE$.

  Remarquons que $\Delta AEB$ et $\Delta CED$ ont $CD=AB$ et $\angle AEB = \angle CED$. Par conséquent, ce sont des triangles congruents. Donc, nous avons que $$ DE=BE=x \,. $$ Ce qui implique aussi que $$ AE=CE=a-x \,. $$ Par le théorème de Pythagore, nous obtenons que $$ (a-x)^2+b^2=x^2 \, \Rightarrow \, x=\frac{a^2+b^2}{2a} \,. $$ Dans le triangle $\Delta BED$, $DC=b$ est la hauteur associée au côté $BE=x$. Alors $$ \mbox{Aire} (BED)=\frac{bx}{2}= \frac{b}{4a} \left(a^2+b^2 \right) \,. $$

  ∎