Year: 2023 2022 2021 2020 2019 2018 2017 2016 2015 2014 2013 2012 2021 2020 2019 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2004 2003 2002 2001 2000 1999 1998 1997 1996

• Year:
• 2023
• 2022
• 2021
• 2020
• 2019
• 2018
• 2017
• 2016
• 2015
• 2014
• 2013
• 2012
• 2011
• 2010
• 2009
• 2008
• 2007
• 2006
• 2005
• 2004
• 2003
• 2002
• 2001
• 2000
• 1999
• 1998
• 1997
• 1996

Week 9

• Problem (posted October 29th)

  In triangle $\Delta ABC$ we denote as usual $AB=c, AC=b, BC=a$. Let $D$ be the point on the side $BC$ such that $AD$ is the bisector of $\angle BAC$. Let $E$ be point symmetric to $D$ with respect to the midpoint $M$ of $BC$, and let $F$ be the point inside the segment $BC$, such that $\angle BAF =\angle EAC$. Show that $$ \frac{BF}{FC}=\frac{c^3}{b^3} \,. $$

• Solution (posted November 5th)

  Problem 4 of the 30th Spanish Mathematical Olympiad, First Round, 1993 , which appeared in Crux Mathematicorum [1998: 69]. We present the solution by Toshio Seimiya, which appeared at [1999: 201-203].

  Note: An extended video solution to this problem is also available and includes an alternative solution involving the Law of Sines.

  Let $T$ be the point on $AF$ so that $BT \parallel AC$ and let $S$ be the point on $AE$ so that $CS \parallel AB$.

  

  Then \begin{align} \angle ABT&+\angle BAC=180^\circ \cr \angle ACS&+\angle BAC=180^\circ \,. \end{align} Then, $\angle ABT = \angle ACS$ and $\angle BAT =\angle CAS$ showing that $\Delta BAT \sim \Delta CAS$. This gives \begin{equation}\tag{1} \frac{AT}{AS}=\frac{BT}{CS}=\frac{c}{b} \,. \end{equation}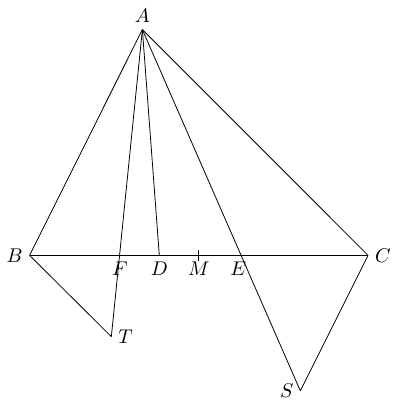

  As $BT \parallel AC$ we get $\Delta BFT \sim \Delta CFA$ and hence \begin{equation}\tag{2} \frac{BF}{FC}=\frac{FT}{AF}=\frac{BT}{b} \,. \end{equation}

  Similarly, $CS \parallel AB$ implies $\Delta ABE \sim \Delta CSE$ and hence \begin{equation}\tag{3} \frac{BE}{CE}=\frac{AE}{SE}=\frac{c}{CS} \,. \end{equation}

  Since $E$ is the symmetric of $D$ with respect to $M$ we have $EC=BD$ and $BE=CD$, and hence $$ \frac{BE}{EC}=\frac{DC}{DB} \,. $$

  Finally, since $AD$ is the bisector of $\angle BAC$, the Bisector Theorem gives \begin{equation}\tag{4} \frac{DC}{DB}=\frac{b}{c} \,. \end{equation}

  Combining (3) and (4) we get $$ \frac{c}{CS}=\frac{b}{c} \Rightarrow CS=\frac{c^2}{b} \,. $$ Therefore, by (1) we get $$ BT=\frac{c^3}{b^2} \,. $$

  Finally, (2) gives $$ \frac{BF}{FC}=\frac{BT}{b}=\frac{c^3}{b^3} \,. $$ ∎

Week 8

• Problem (posted October 22nd)

  Let $a_1,a_2,..., a_n, b_1, b_2,...b_n$ be $2n$ real numbers such that $a_1,a_2,..., a_n$ are distinct. If there exists a real number $\alpha$ such that for each $1 \leq j \leq n$ we have $$ (a_j+b_1)\cdot(a_j+b_2) \cdot \dots \cdot (a_j+b_n) =\alpha \,, $$ show that there exists a number $\beta$ such that for each $1 \leq k\leq n$ we have $$ (a_1+b_k)\cdot(a_2+b_k) \cdot \dots \cdot (a_n+b_k) =\beta \,. $$

• Solution (posted October 29th)

  Problem 2 of the Second paper, Sixth Irish Mathematical Olympiad, which appeared in Crux Mathematicorum [1995: 152]. We present the solution by Michael Selby, which appeared at [1997: 141-142].

  Note: A video solution to this problem is also available.

  Define $$ P(X)=(X+b_1)\cdot(X+b_2)\cdot \dots \cdot (X+b_n) -\alpha\,. $$ Then, $P(a_1)=P(a_2)=...=P(a_n)=0$. Therefore, since $a_1,a_2,...,a_n$ are dintinct, by the Factor Theorem we have $$ P(X)=(X-a_1)\cdot(X-a_2) \cdot \dots \cdot (X-a_n) \,. $$ This gives \begin{equation}\tag{1} (X+b_1)\cdot(X+b_2)\cdot \dots \cdot (X+b_n) -\alpha=(X-a_1)\cdot(X-a_2) \cdot \dots \cdot (X-a_n) \,. \end{equation} Now, for each $1 \leq k \leq n$, setting $X=-b_k$ in (1) gives $$ 0-\alpha=(-1)^{n} (a_1+b_k)\cdot(a_2+b_k) \cdot \dots \cdot (a_n+b_k) \,. $$ Therefore, for all $1 \leq k \leq n$ we have $$ (a_1+b_k)\cdot(a_2+b_k) \cdot \dots \cdot (a_n+b_k) = (-1)^{n+1} \alpha \,. $$ Setting $\beta=(-1)^{n+1} \alpha$ gives the claim.

Week 7

• Problem (posted October 15th)

  An equilateral triangle of side length $6$ is divided into $36$ small equilateral triangles of side length $1$. We construct pieces of type $A$ and type $B$ by joining triangles of side length $1$, as in the diagram below. By using $m$ pieces of type $A$ and n pieces of type $B$, with no overlapping and no gaps, like the pieces of a jigsaw puzzle, we can construct the original large triangle. Determine all possible values of $m$.

  

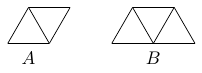
• Solution (posted October 22nd)

  Problem 2 Olimpiada Nacional Escolar de Matematica 2009, Level 2, which appeared in Crux Mathematicorum at [2010: 373]. We present the solution by Chip Curtis, which appeared at [2011: 425-426], modified by the editor.

  Note: A video solution to this problem is also available.

  Since each piece of type $A$ covers two triangles, and each piece of type B covers three triangles, we have $$ 2m+ 3n = 36 \,. $$ This yields $$ m \in \{ 0, 3, 6, 9, 12, 15, 18 \} \,. $$ We prove that $m = 0, 3, 6, 9$ are possible, while $m = 12, 15, 18$ are impossible.

  The following pictures show that $m=0,3,6,9$ are possible.

  

  

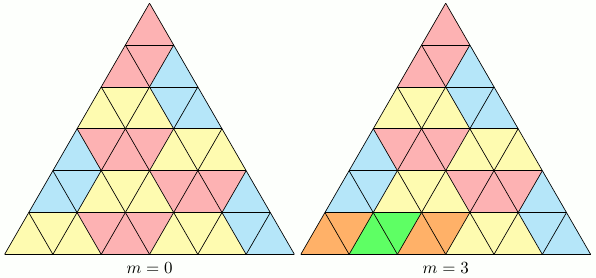
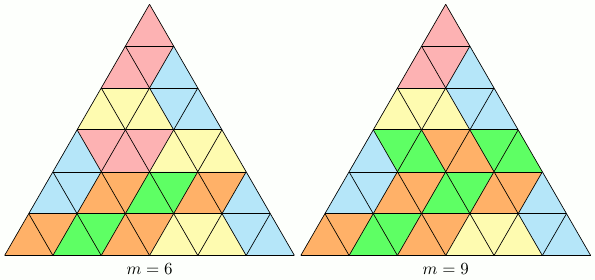
  To see that $m = 12, 15, 18$ are impossible, color the small triangles with two colors alternately.

  

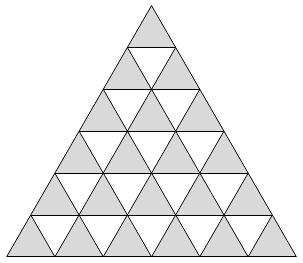
  Note that any piece of type $A$ covers exactly one white and one gray triangle. Any piece of type $B$ covers either two white and one gray triangles, or one white and two gray triangle.

  Since there are 6 more gray triangle than white triangles, we need to use at least $6$ pieces of type $B$, that is $n \geq 6$. Therefore $$ m=\frac{36-3n}{2} \leq \frac{36-18}{2} =9 \,. $$

  This shows that $$ m \in \{ 0, 3, 6, 9 \} \,. $$

Week 6

• Problem (posted October 8th)

  Find all the functions $f : \mathbb R \to \mathbb R$ with the property that for all $x,y \in \mathbb R$ we have \begin{equation}\tag{1} f \left(xf(x)+f(y) \right)= \left(f(x) \right)^2+y .\end{equation}

• Solution (posted October 15th)
  Note: A video solution to this problem is also available.

  Problem 1 of the 17th Balkan Mathematical Olympiad , which appeared in Crux Mathematicorum [2004: 84]. We present the solution by José Luis Díaz-Barrero, which appeared at [2005: 523-524].

  It is easy to see that the function $f(x)=x$ for all $x \in \mathbb{R}$ and the function $f(x)=-x$ for all $x \in \mathbb{R}$ satisfy (1). We show that these are the only solutions.

  Let $a=f(0)$. Setting $x=0$ in (1) we get \begin{equation}\tag{2} f(f(y))=y+a^2 \,. \end{equation} Pick $b=f(-a^2)$. Then $f(b)=f(f(-a^2))=-a^2+a^2=0$.

  Setting $x=b$ in (1) we get \begin{equation}\tag{3} f(f(y))=y \,. \end{equation} By combining (2) and (3) we get $a=0$, and hence $f(0)=0$. Setting $y=0$ in (1) we get \begin{equation}\tag{4} f(xf(x))=\left( f(x) \right)^2 \,. \end{equation}

  Now, let $t \in \mathbb R$ be arbitrary. Setting $x=f(t)$ in (4), and using the fact that by (3) we have $f(x)=t$ we get \begin{equation}\tag{5} f(tf(t))=\left( f(f(t)) \right)^2=t^2 \,. \end{equation}

  Therefore, for all $x \in \mathbb R$ we have by (4) and (5) \begin{equation}\tag{6} x^2=f(xf(x))=(f(x))^2 \,. \end{equation}

  This gives that $f(x)=\pm x$ for each $x \in \mathbb{R}$. Therefore, for each $x \in \mathbb{R}$ we have either $f(x)=x$ or $f(x)=-x$. To complete the solution we need to show that the sign is the same for all $x$.

  Assume by contradiction that there exist non-zero numbers $\alpha, \beta$ such that $f(\alpha)=\alpha$ and $f(\beta)=-\beta$. Then, setting $x=\alpha, y=\beta$ in (1) we get $$ f \left(\alpha^2-\beta \right)= \alpha^2+\beta \,, $$ and hence, by (6) $$ \left(\alpha^2-\beta \right)^2=\left(\alpha^2+\beta \right)^2 \,. $$ Expanding, we get $\alpha^2 \beta=0$ which contradicts the fact that $\alpha, \beta$ are non-zero.

  Since we got a contradiction, our assumption was wrong. Therefore, the only solutions are the function $f(x)=x$ for all $x \in \mathbb{R}$ and the function $f(x)=-x$ for all $x\in \mathbb{R}$.

  Editor's note: This problem is similar to the 2014 COMC Problem of the Week 4, see https://comc.math.ca/2014/potw.html

Week 5

• Problem (posted October 1st)

  Find all the triplets $(x,y,z)$ consisting of positive integers, which satisfy the equation $$ \frac{1}{x}+\frac{2}{y}-\frac{3}{z}=1 $$

• Solution (posted October 8th)

  Problem 3 of the 26th Belgian Mathematical Olympiad , which appeared in Crux Mathematicorum [2004: 268]. We present the solution by Pierre Bornsztein, which appeared at [2006: 153].

  Note: A video solution to this problem is also available.

  Let $(x,y,z)$ be any solution to the equation. Then \begin{equation}\tag{1} yz+2xz=3xy+xyz \,. \end{equation} If $x \geq 3$ and $y \geq 3$ then $3(x-1)\geq2x$ and hence $$ 3xy+xyz> xyz = yz +(x-1)yz \geq yz+3(x-1)z \geq yz+2xz \,, $$ which contradicts (1). Therefore, $x <3$ or $y<3$.

  • First suppose that $y \geq 3$. Then $x=1$ or $x=2$.

    If $x=2$ then $$ yz+4z=6y+2yz \Rightarrow yz+6y-4z=0 \Rightarrow (y-4)(z+6)=-24 \,. $$ Since $y-4 \geq -1$ and $z+6 \geq 7$ we get $y-4=-1$ and $z+6=24$ giving the solution $$ (x,y,z)=(2,3,18) \,. $$ It is easy to check that this is a solution.

    If $x=1$ then $$ yz+2z=3y+yz \Rightarrow 3y= 2z $$ giving the solutions $$ (x,y,z)=(1,2a,3a) \,, $$ for an integer $a \geq 2$ (since $y \geq 3$).

    It is easy to check that all these are solutions.

  • If $y=2$ then the equation becomes $$ 2z+2xz=6x+2xz \Rightarrow z=3x \,. $$ This gives the solutions $$ (x,y,z)=(b,2,3b) \,, $$ for an integer $b \geq 1$. Note that for $b=1$ we get the solution $(1,2,3)$, which corresponds to $a=1$ in the previous paragraph.
  • If $y=1$ then the equation becomes $$ z+2xz=3x+xz\Rightarrow xz-3x+z=0 \Rightarrow (x+1)(z-3)=-3 \,. $$ Since $x+1 \geq 2$ we have $x+1=3, z-3=-1$, giving the solution $$ (x,y,z)=(2,1,2) \,. $$ Conversely, the triple $(2,1,2)$ is a solution.

    Therefore, the solutions are all the triples of the form $(1, 2a, 3a), (a, 2, 3a)$ for positive integer $a$, together with $(2,1,2)$ and $ (2,3,18)$.

Week 4

• Problem (posted September 24th)

  If $$\left(x+\sqrt{x^2+1}\right)\left(y+\sqrt{y^2+1}\right)=1$$ show that $x+y=0$.

• Solution (posted October 1st)

  Problem 2 of the 31st Spanish Mathematical Olympiad, First Round, which appeared in Crux Mathematicorum [1998: 453]. We present the solution by Mohammed Aassila, which appeared at [2000: 142], modified by the editor.

  Note: A video solution to this problem is also available.

  Set $z=x+\sqrt{x^2+1}$. Then, $z>0$ and $$ \frac{1}{z}=\frac{\sqrt{x^2+1}-x}{x^2+1-x^2}=\sqrt{x^2+1}+x-2x=z-2x \,, $$ giving $$ x=\frac{z^2-1}{2z} \,. $$ Then, \begin{align} z\left(y+\sqrt{y^2+1}\right)&=1 \qquad \Rightarrow \cr y+\sqrt{y^2+1}&=\frac{1}{z} \qquad \Rightarrow \cr z=\frac{\sqrt{y^2+1}-y}{y^2+1-y^2}&=\sqrt{y^2+1}+y-2y=\frac{1}{z}-2y \Rightarrow \cr y&=\frac{1-z^2}{2z} \,. \end{align} Hence $$ x+y= \frac{z^2-1}{2z} + \frac{1-z^2}{2z} =0 \,. $$

  ∎

  Editor's note: If you are familiar with logarithms and inverse hyperbolic functions, you will probably like Michel Battaille's solution: Taking logarithms and using $\sinh^{-1}(x)=\ln\left(x+\sqrt{x^2+1}\right)$ the equation becomes $$ \sinh^{-1}(x)+\sinh^{-1}(y) =0 \,. $$ Since $\sinh^{-1}(x)$ is an odd function, and one-to-one, we get $$ \sinh^{-1}(x)=\sinh^{-1}(-y) \Rightarrow x=-y \,. $$

Week 3

• Problem (posted September 17th)

  Define the sequence $a_1, a_2 , a_3 , \dots$ as follows

  $a_1$	$=a_2=1003 $
  $a_{n+1}$	$=a_n-a_{n-1} \qquad$ for all $n \geq 2 \,.$

  Calculate the sum of the first 2006 terms in the sequence.

• Solution (posted September 24th)

  Problem 3 of the Mathematical Olympiad of the Asociación Venezolana de Competencias Matemáticas, 2006, which appeared in Crux Mathematicorum [2009: 380]. We present the solution by Oliver Geupel, which appeared at [2011: 278].

  Note: A video solution to this problem is also available.

  We have

  $a_3$	=$a_2-a_1=0$
  $a_4$	=$a_3-a_2=-1003$
  $a_5$	=$a_4-a_3=-1003$
  $a_6$	=$a_5-a_4=0 $
  $a_7$	=$a_6-a_5=1003=a_1$
  $a_8$	=$a_7-a_6=1003=a_2$

  It follows from here that the sequence is periodic, with period $6$. Moreover, the sum of 6 consecutive terms is zero.

  Therefore, as $2004=6 \cdot 334$ we get

  $\displaystyle\sum_{k=1}^{2006}a_k$	$\displaystyle =a_1+a_2 + \sum_{j=0}^{333} \left( a_{6j+3}+a_{6j+4}+a_{6j+5}+a_{6j+6}+a_{6j+7}+a_{6j+8} \right)$
  	$=a_1+a_2$
  	$=2006 \,.$ ∎

Week 2

• Problem (posted September 10th)

  How many subsets with three elements can be formed from the set $\{ 1 , 2 , 3, \dots , 20 \}$ such that $4$ is a factor of the product of the three numbers in the subset?

• Solution (posted September 17th)

  Problem 1 of the Icelandic Mathematical Contest 2004-05, which appeared in Crux Mathematicorum [2008: 285]. We present the solution by John G. McLoughlin which appeared at [2009: 386].

  Note: A video solution to this problem is also available.

  There are $\binom{20}{3}=1140$ subsets of three elements in total. We count how many do not meet the requirements.

  We first note that a subset meets the requirements excepting in two cases:

  • all elements are odd.
  • two elements are odd, and the third is even but not a multiple of $4$.

  In the first case, there are $\binom{10}{3}=120$ subsets consisting of only odd numbers.

  In the second case, there are $\binom{10}{2}\binom{5}{1}=225$ subsets consisting of two odd numbers and one even number not divisible by $4$.

  Therefore, in total there are $$ 1140-120-225=795 $$ such subsets. ∎

Week 1

• Problem (posted September 3rd)

  We give two entry level problems this week. Give them a try. Look for the source and the solution next week!

  Problem A
  Let $x$ be an integer of the form $$ x=\underbrace{111\dots11}_{n \mbox{ times }} $$ Show that, if $x$ is prime then $n$ is prime.

  Problem B
  Given a rectangle with sides $a$ and $b$, with $a>b$, fold it along the diagonal. Determine the area of the overlapping triangle (the shaded area in the picture).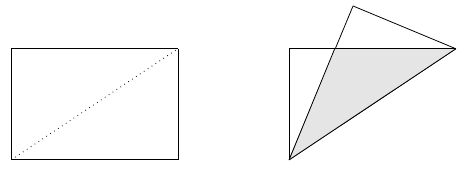

  

• Solution (posted September 10th)

  Problem A

  Problem 7 of the Chilean Mathematical Olympiads 1994-95, which appeared in Crux Mathematicorum [2001: 170]. We present the solution by Christopher J. Bradley that appeared at [2003: 294].

  Note: A video solution to this problem is also available.

  Note that $$ 9x=\underbrace{999\dots 99}_{n \mbox{ times }}=10^n-1 \,. $$ Therefore, $$ x=\frac{10^n-1}{9} \,. $$ Now, if we assume by contradiction that $n$ is composite, $n=n_1n_2$ for some $n_1, n_2 >1$. Then $$ x=\frac{10^n-1}{9}=\frac{10^{n_1}-1}{9} \left(1+10^{n_1}+10^{2n_1}+\dots+10^{n_1(n_2-1)} \right)\,. $$ As $\frac{10^{n_1}-1}{9}$ is an integer greater than $1$ and $1+10^{n_1}+10^{2n_1}+\dots+10^{n_1(n_2-1)}>1$ we get that $x$ is composite, a contradiction.

  Since, we got a contradiction, our assumption that $n$ is composite is wrong.

  Therefore, $n$ is not composite and $n\neq 1$ (since $x=1$ is not prime), which proves that $n$ is prime. ∎

  Editor's note: Primes of this form are sometimes called "repunit primes". So far 5 repunit primes are known, namely the values of $x$ for $n \in \{ 2, 19, 23, 317, 1031 \}$. The values of $x$ for $n \in \{ 49081, 86453, 109297, 270343\}$ are also believed to be prime.

  Problem B

  Problem 1 of the XV Gara Nazionale di Matematica 1999, which appeared in Crux Mathematicorum [2002: 481] . We present the solution by Bob Serkey that appeared at [2005: 37].

  Note: A video solution to this problem is also available.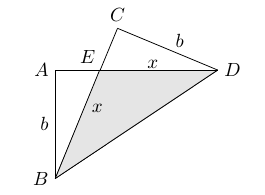

  

  Let $E$ be the intersection of $BC$ and $AD$, and let $x=BE$.

  Note that the right triangles $\Delta AEB$ and $\Delta CED$ have $CD=AB$ and $\angle AEB = \angle CED$, and thus are congruent. Therefore, we have $$ DE=BE=x \,. $$ We therefore also have $$ AE=CE=a-x \,. $$ By Pythagoras theorem we have $$ (a-x)^2+b^2=x^2 \, \Rightarrow \, x=\frac{a^2+b^2}{2a} \,. $$ In the triangle $\Delta BED$, $DC=b$ is the altitude to the base $BE=x$. Therefore $$ \mbox{Area} (BED)=\frac{bx}{2}= \frac{b}{4a} \left(a^2+b^2 \right) \,. $$

  ∎