1998-1999 Olympiad Correspondence Problems

Set 3

13.

The following construction and proof was proposed for trisecting a given angle with ruler and Criticizecompasses the arguments.

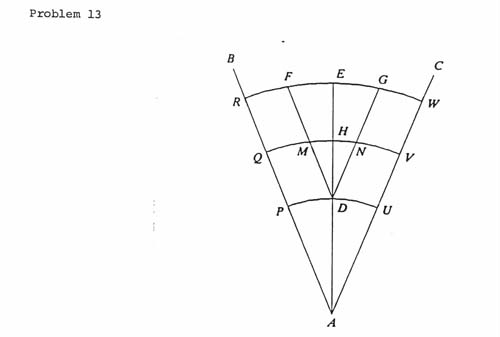
Construction. Let the angle to be trisected be BAC. With center A and respective radii of two, three and four units, draw arcs PU, QV and RW to intersect the arms of the angle. Determine D, E, F and G, the respective midpoints of arcs PU, RW, RE and EW. Let M and N be the respective intersections of the segments FD and GD with the arc QV. Then the rays MA and NA yield the desired trisection of angle BAC.

First proof. Let H be the midpoint of arc QV. Consider the ``triangles'' DMH and DFE, one side of each being a circular arc. Since the arcs RW and QV are parallel, ÐDFE = ÐDMH and ÐDEF = ÐDHM, so that triangle DMH is similar to triangle DFE. Since 2DH = DE, it follows that arc MN = 2 arc MH = arc FE. Now, arc QV = (3/4) arc RW = 3 arc FE and arc QM = arc NV. Therefore, the arc QV is trisected by M and N, and so the construction is valid. QED

Second proof. Since arc RW = 2 arcPU, arc PD = arc RF. Therefore, FD is parallel to RP, and so arc QM = arc RF. Similarly, arc NV = arc GW = arc RF. Since arc QV = 3 arc RF, QV is trisected by M and N. QED

View solution

14.

The following construction was proposed for ``squaring the circle'' with ruler and compasses, i.e., constructing a square of equal area to a given circle. Criticize the proposed construction. You can take it for granted that it is possible to construct a square equal in area to a given quadrilateral.

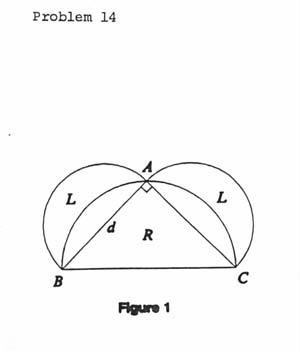
Suppose we are given a circle of diameter d. The problem is to show that, using ruler and compasses, we can construct a square of area equal to that of a circle. As in the figure, construct an isosceles right triangle ABC whose equal sides have length d. Let the hypotenuse BC be the diameter of a semi-circle passing through A, and let semi-circles also be constructed on diameters AB and AC. The area of the larger semi-circle is equal to twice that of each of the smaller, and it is not hard to argue that the sum of the areas of the two lunes (marked L) is equal to the area of the triangle (marked R).

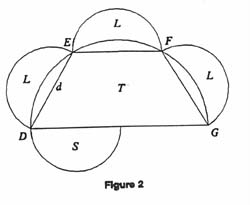
Now construct a trapezoid DEFG which is the upper part of a regular hexagon of side d. Thus DG = 2DE = 2EF = 2FG = 2d. The area of the semi-circle with diameter DG is four times the area S of the semi-circle of diameter d constructed on each of the sides DE, EF, FG as diameter. It can be seen that the area S plus the area of the three lunes (L) is equal to the area of the trapezoid (T).

Symbolically, we have R = 2L and T = 3L + S. Hence the area of the given circle is 2S = 2T - 6L = 2T - 3R. Thus, we have been able to construct rectilinear figures some linear combination of which will yield the area of the circle. It is known that one can construct with ruler and compasses a square whose side is equal to 2T - 3R.

View solution

15.

A faulty proof is given for the following result. Find the flaw in the proof and give a correct argument.

Proposition. If in a triangle two angle bisectors are equal, then the triangle is isosceles.

Proof. Let BAC be the triangle and AN, CM the two equal bisectors, with N and M on BC and AB respectively. Suppose the perpendicular bisectors of AN and CM meet at O. The circle with center O passes through A, M, N, C. Angles MAN and MCN, subtended by MN are equal. Hence, the angles BAC and BCA are equal, and the result follows. QED

View solution

16.

Criticize the solution given to the following problem and find a correct solution.

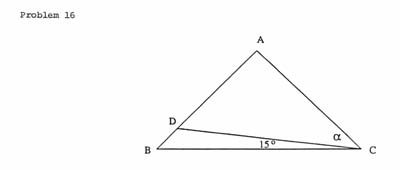
Problem. ABC is an isosceles triangle with AB = AC. The point D is selected on the side AB so that ÐDCB = 15^° and BC = Ö6 AD. Determine the degree measure of ÐBAC.

Solution. Let AB = AC = 1 and let ÐDCA = a, where 0 < a < 75^°. Then BC = 2cos(15^° + a). The Sine Law applied to triangle ADC yields

1 sin(30° + a) = CD sin(150° - 2a)

whence

CD = sin(150° - 2a) sin(30° +a)   .

Applying the Sine Law to triangle DBC yields

2cos(15° + a) sin(30° + a) = BC sin(150° - a) = CD sin(15° + a) = sin(150° - 2a) sin(15° + a) sin(30° + a)   .

Hence

sin(30° + 2a) = 2cos(15° + a)sin(15° + a) = sin(150° - 2a)

so that 30^° + 2a = 150^° - 2a with the result that a = 30^°. Hence ÐBAC = 150^° - 2a = 90^°. QED

This checks out: BC = Ö2 and AD = 1/Ö3.

View solution

17.

Criticize the solution given to the following problem and determine a correct solution.

Problem. Let A¢, B¢ and C¢ denote the feet of the altitudes in the triangle ABC lying on the respective sides BC, CA and AB, respectively. Show that AC¢ = BA¢ = CB¢ implies that ABC is an equilateral triangle.

Solution. Let k = AC¢ = BA¢ = CB¢ and let u = CA¢, v = AB¢, w = BC¢. By the Law of Cosines,

(k+u)2 = (k+v)2 + (k+w)2 - 2(k+v)(k+w)cosA

whence

(1 - 2cosA)k2 + 2((v+w)(1 - cosA) - u)k + (v2 + w2 - u2 - 2vwcosA) = 0  .

Equating coefficients to zero yields in particular that 1 - 2cosA = 0 or q = 60^°. QED

View solution

18.

Analyze the solution of the following problem. In the days before calculus, one way to check the tangency of two curves with algebraic equations f(x, y) = 0 and g(x, y) = 0 at a common point (a, b) was to eliminate one of the variables from the system of two equations and to check whether the resulting equation in the other variable had a double root corresponding to the common point. As a simple example, y = x² and y = 2x - 1 represent curves tangent at (1, 1) because x² = 2x - 1 has a double root at x = 1.

Problem. Find all values of k for which the curves with equations

y = x2 + 3       and        x2 4 + y2 k = 1

are tangent.

Solution. Eliminating x yields the equation

4y2 + ky - 7k = 0       (1)

for the ordinates of the intersection points of the two curves. If the curves are to be tangent, the quadratic equation should have a double root, so that its discriminant k² + 112k vanishes. Since k = 0 is not admissible, k must be -112. QED

With the aid of a sketch, it is not hard to see that k = 9 also works. Why is it not turned up by this argument?

View solution

---

Problem 13.

13.

First solution. In the first solution, the assertion that the two ``triangles'' with common vertex are similar is confounded by the fact that the curved lines are not arcs of circles with their centres at the common vertex, so that there is no similarity transformation which takes one to the other. For suppose otherwise. They would have to be related by a similarity transformation with centre D which carries E to H. The factor of this similarity would have to be ¹/₂. The arc FE would have to be carried to an arc through H whose centre is the midpoint of AD; such an arc would intersect FD at a point X strictly between M and D, and arc XH would equal half arc FE. Thus, MH is not the image of FE under the similarity and we are led to a contradiction.

As for the second solution, note that two lines are parallel if and only if there is a translation of the plane that takes one to the other. Consider a translation that takes PR to a parallel line passing through D so that P ® D. Since chord RE is the image of chord PD under a dilation with factor 2, RE is parallel to PD and is twice as long. Hence R gets carried by the translation to the midpoint of Y of chord RE. Now the line FY passes through the point A, so that F, Y and D are not collinear. Since DY is parallel to PR, DF is not parallel to PR.

13.

Second solution. The angle between two curves at a point is defined to be the angle between the tangents to the curves at the point. Consider the dilation with centre A and factor 3/4. It takes arc RW to arc QV and the point F to the midpoint J of arc QH. Note that J ¹ M. Thus, the tangent to arc RW at F goes to the (parallel) tangent to arc QH through J, and so the tangent to arc RW at F is not parallel to the tangent to arc QH through M. Therefore ÐDFE ¹ ÐDMH contrary to the assertion of the proof. (Note however that ÐDEF = ÐDHM = 90^°.)

13.

Third solution. We look at the first proof and find a contradiction. Consider the assertion that the triangles DMH and DFE are similar. This would imply that DM:MF = DH:HE = 1:1. Let us assign coordinates so that A ~ (0, 0), D ~ (0, 2), H ~ (0, 3) and E ~ (0, 4). Let y = mx be the equation of the line DF and suppose that it meets QV in M ~ (p, mp+2) and RW in F ~ (q, mq+2). The condition DM = MF entails that DF = 2DM or (1 + m²)q² = 4(1 + m²)p² so that q = 2p.

Now M lies on the circle of equation x² + y² = 9 so that Now M lies on the circle of equation x² + y² = 9 so that (1 + m²)p² + 4mp = 5. Similarly, (1 + m²)q² + 4mq = 12. Substituting q = 2p yields 4(1+m²)p² + 8mp = 12. Eliminating terms in p² gives 8mp = 8 which leads to p² + 5 = 5 or p = 0. But this is a contradition, as M is not collinear with ADE.

---

Problem 14.

14.

First solution. The difficulty in the construction is that the shorter arcs with the congruent chords in the two figures arise from circles with different radii, so that the lunes for one figure are not congruent to the lunes for the other. it can be checked that the lunes on the right triangle have area ¹/₄r² while those on the sides of the hexagon have area ((Ö3/4) - (p/2))r².

---

Problem 15.

15.

First solution. The right bisectors of the two equal angle bisectors AN and CM meet at O. However, there is no guarantee that O is equidistant from AN and CM. Therefore, we cannot claim without further justification that the circle with centre O that contains A and N is the same as the circle with centre O that contains C and M.

Let a, b, c, m, n be the respective lengths of BC, AC, AB, CM, BN. Since AM:MB = b:a and AM + MB = AB, we find that

|AM | = bc a+b      |BM | = ac a + b  .

Similarly

|CN | = ba b+c      |BN | = ca b+c  .

Applying the Law of Cosines to triangle AMC and BMC with q = ÐAMC yields

b2 = m2 + æ ç è bc a+b ö ÷ ø 2   - 2mbc a+b cosq

a2 = m2 + æ ç è ac a+b ö ÷ ø 2   + 2mac a+b cosq

whence

b2 a + a2 b = m2 (a + b) + abc2(b+a) (a+b)2

or

m2 = ab é ê ë 1 - c2 (a+b)2 ù ú û  .

Similarly

n2 = bc é ê ë 1 - a2 (b+c)2 ù ú û  .

Suppose that m = n. Then

a - c = ac æ ç è c (a+b)2 - a (b+c)2 ö ÷ ø  .

If, for example, a > c, then the left side would be positive and the right side negative, a contradition. Similarly, a < c leads to a contradiction. Hence, a = c.

---

Problem 16.

16.

The answer checks out, and BC = Ö2, AD = 1/Ö3. However, the argument does not use the information about the ratio of BC and AD, and so applied whenever ÐDCB = 15^°. The equation sin(30^° + 2a) = sin(150^° - 2a) has two possible consequences: either 30^° + 2a and 150^° - 2a are equal or they sum to 180^°. But the latter is always true, so the argument really makes no progress towards the desired result.

First solution. Let v and u be the respective lengths of CD and AD. By the Law of Sines applied to triangles DBC and ADC, we find that

v u = Ö6 sin(15° + a) sin(30° + a) = sin(30° + 2a) sina

where v and u are the respective lengths of CD and AD. This simplifies to

Ö6 sina = 2cos(15°+ a)sin(30° + a) = sin(45° + 2a) + sin15° .

Letting q = a+ 15^°, we find that

(Ö6 - 2cosq) sinqcos15° = (Ö6 + 2cosq) cosqsin15° .

Now

æ ç è Ö6 - 2cosq Ö6 + 2cosq ö ÷ ø tanq

is an increasing function of q for 0 < q < 90^°, and, when q = 45^°, it assumes the value

Ö6 - Ö2 Ö6 + Ö2 = 2 -Ö3 = tan15° ,

so that the equation is satisfied only for the acute angle q = 45^°. This yields a = 30^° and ÐBAC = 90^°.

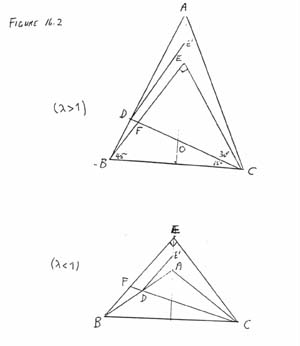
16.

Second solution. See Figure 16.2. Construct triangle BEC and a point F on BE such that ÐBEC = 90^°, EB = EC and ÐBCF = 15^°. Then

EF = EC tan30° = BC cos45° tan30° = BC/Ö6 = DA .

Also, C,F,D are collinear, and A and E lie on the right bisector of BC. Let O be the intersection of this right bisector and CD.

The dilation with centre O and some factor l that takes F to D also take E to a point E¢ on the right bisector with FE || DE¢. If l > 1, then FE = DA > DE¢ = lFE, while if l < 1, then FE = DA < DE¢ = lFE. In both cases we get a contradiction, so that l must equal 1. Thus, F = D, E = E¢ = A. The result follows.

---

Problem 17.

17.

The equation resulting from the Law of Cosines is a conditional equation involving the variables and not an identity, in particular not an identity in k. Hence the vanishing of the left side does not entail the vanishing of the coefficients of the various powers of k.

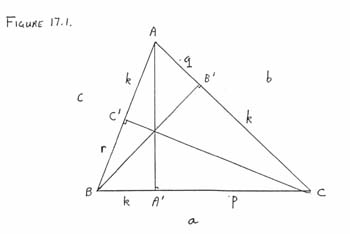
First solution. See Figure 17.1. The area of the triangle is half of

a   ______ Öc2 - k2   = b   ______ Öa2 - k2   = c   ______ Öb2 - k2

from which

a2 c2 - a2 k2 = a2 b2 - b2 k2 = b2 c2 - c2 k2 .

hence

a2(c2 - b2) = k2(a2 - b2)   b2 (a2 - c2) = k2 (b2 - c2)   c2 (b2 - a2) = k2 (c2 - a2) .

Suppose for example that a ³ b. Then a ³ c ³ b from the first and third of these equations. But then from the middle equation, a = b = c and the result follows.

17.

Second solution. As in the first solution, we have that

a2(c2 - b2) a2 - b2 = b2(a2 - c2) b2 - c2

whence 3a² b² c² = a² c⁴ + b² a⁴ + c² b⁴. >From the AM-GM Inequality, 3a² b² c² = a² c⁴ + b² a² + c² b⁴ ³ 3(a⁶ b⁶ c⁶)^1/3 = 3a² b² c², with equality if and only if a = b = c. Hence, in this case, a = b = c.

17.

Third solution. see Figure 17.1. Let p = A¢C, q = B¢A and r = C¢B. From Ceva's Theorem, pqr = k³. Since (q + k)² - p² = (r + k)² - k², we have that

k2 = p2 + r2 - q2 + 2k(r - q) .

Also

k2 = r2 + q2 - p2 + 2k(q - p) ,

k2 = q2 + p2 - r2 + 2k(p - r) .

Adding these equations yields 3k² = p² + q² + r². By the AM-GM Inequality, p² + q² + r² = 3(pqr)^(2/3) = k² with equality if and only if p = q = r. Hence p = q = r = k and the triangle ABC is equilateral.

17.

Fourth solution. See Figure 17.4. [D. Cheung] Let O be the orthocentre of the triangle, s = |A¢C |, u = |C¢O | and |AC¢| = |BA¢| = |CB¢| = 1. Triangles OAC¢ and OCA¢ are similar, so that OA¢: OC¢ = A¢C : AC¢ and |OA¢| = su. Then |OC |² = s² (1 + u²), |OB¢|² = s² (1 + u²) - 1 and |OB |² = 1 + s² u². Since triangles BOC¢ and COB¢ are similar,

BO:OC = OC¢:OB¢ Þ [1+s2u2][s2 + s2u2 - 1] = u2[s2 + s2 u2] Þ (s2 - 1)[1 + s2 u2 + s2 u4] = 0 Þ s = 1 ,

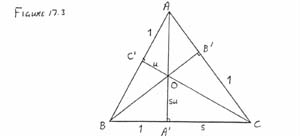x

---

Problem 18.

18.

First solution. Eliminating x from the two equations of the curves yields the equation

4y2 + ky - 7k = 0       (1)

while eliminating the variable y from the two equations yields the equation

4x4 + (24 + k)x2 + (36 - 4k) = 0       (2) .

Observe that (1) is a quadratic in y while (2) is a quartic in x (as well as quadratic in x², each with discriminant k(k+112). In solving for the intersection point, we find that each root of (1) corresponds to a pair of roots of (2) with opposite signs.

Why is tangency not always accompanied by a double root? First, suppose that k is positive, so that the curves are a parabola with its axis along the y-axis and an ellipse centred at the origin. For k < 9, x² must be negative for each root of (2), so that while there is a corresponding real value of y satisfying (1), the values of x are nonreal. Thus, the curves do not intersect. When k > 9, (2) has two roots of opposite sign whose squares are positive and two whose squares are negative. The first two correspond to two points of intersection that have the same y-value. Thus, one of the roots of (1) is a positive value of y giving the ordinate of both intersection points and the other is negative (since their product -7k/4 is negative) and corresponds to no real point of intersection. As k approaches 9, the two intersection points coalesce into one. There is no doubling of the roots of (1), but of course (2) has x = 0 as a double root for k = 9.

Next, suppose that k is negative. To have any real solutions at all, we must have k £ -112. Let k < -112. The curves, a parabola and an hyperbola, have four intersection points, two with positive abscissae and separate ordinates and their reflected images in the y-axis. As k approaches -112, the two positive abscissae and the two ordinates coalesce, and we find that at k = -112, (1) has y = 14 as a double root and (2) has x = Ö[11] and x = Ö[11] both as double roots. In this case, the double root criterion turns out to be valid.