CMS/SMC
Société mathématique du Canada
www.smc.math.ca
  location: 
       
Problem Set 3

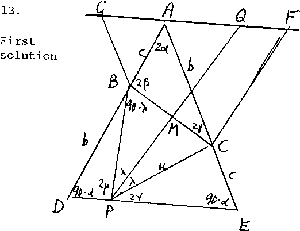
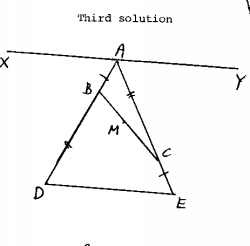
13.
ABC is a triangle and D is a point on AB produced beyond B such that BD = AC, and E is a point on AC produced beyond C such that CE = AB. The right bisector of BC meets DE at P. Prove that ÐBPC = ÐBAC.
(Note: This is Problem 2244 in CM+MM, May, 1997.)
View solution
14.
(a) Let a > b > c > d > 0 and a + d = b + c. Show that ad < bc.
(b) Let a, b, p, q, r, s be positive integers for which
p
q
 < a
b
 < r
s
and qr - ps = 1. Prove that b ³ q + s.

View solution

15.
The Fibonacci sequence { Fn } is defined by F1 = F2 = 1 and Fn+2 = Fn+1 + Fn for n = 0, ±1, ±2, ±3, ¼. The real number t is the positive solution of the quadratic equation x2 = x + 1.
(a) Prove that, for each positive integer n, F-n = (-1)n+1 Fn.
(b) Prove that, for each integer n, tn = Fn t+ Fn-1.
(c) Let Gn be any one of the functions Fn+1Fn, Fn+1Fn-1 and Fn2. In each case, prove that Gn+3 + Gn = 2(Gn+2 + Gn+1).
View solution
16.
(a) Show that, if
cosa
cosb
 + sina
sinb
 = -1  ,
then
cos3 b
cosa
 + sin3 b
sina
 = 1  .

(b) Give an example of numbers a and b that satisfy the condition in (a) and check that both equations hold.
View solution
17.
The sequence of functions { Pn } satisfies the following relations:
P1 (x) = x ,           P2 (x) = x3 ,
Pn+1(x) = Pn3 (x) - Pn-1(x)
1 + Pn (x) Pn-1(x)
   ,        n = 1, 2, 3, ¼.
Prove that all functions Pn are polynomials.
View solution

18.
Each point in the plane is coloured with one of three distinct colours. Prove that there are two points that are unit distant apart with the same colour.
View solution


Solutions to Problem Set 3


13.

13.
First solution. Let the lengths a, b, c, u and the angles a, b, g, l, m, n be as indicated in the diagram.
In the solution, we make use of the fact that if p/q = r/s, then both fractions are equal to (p+r)/(q + s). Since ÐDBP = 90° + l- 2b, it follows that
2m = 180° - (90° - a) - (90° +l- 2b) = a+ 2b- l  .
Similarly, 2n = a+ 2g- l. Using the Law of Sines, we find that
a
sin2a
 = b
sin2b
 = c
sin2g
= b+c
sin2b+ sin2g
 = b+c
2sin(b+ g)cos(b- g)
= b+c
2cosacos(b- g)
  .
Hence
a
sina
 = b+c
cos(b- g)
  .

Since a = 2usinl and, by the Law of Sines,
u
sin(90° - a)
 = b
sin2m
     and     u
sin(90° - a)
 = c
sin2n
   ,
we have that
a
2sinlcosa
= u
cosa
 = b
sin2m
 = c
sin2n
 = b+c
sin2m+ sin2n
= b+c
2sin(m+ n) cos(m- n)
 = b+c
2coslcos(b- g)
 = a
2coslsina
   .
Hence tana = tanl and so a = l.

13.
Second solution. Let M be the midpoint of BC. A rotation of 180° about M interchanges B and C and takes E to G, D to F and P to Q. Then AB = CE = BG and AC = BD = CF. Join GA and FA. Let 2a = ÐBAC. Since AE || BG and AB is a transversal, ÐGBA = ÐBAC = 2a. Since AB = BG, ÐBGA = 90°- a. But ÐBGF = ÐCED = 90° - a. Thus, G, A, F are collinear.
Since GF and DE are equidistant from M, we can use Cartesian coordinates with the origin at M, the line y = 1 as GF and the line y = -1 as DE. Let A ~ (a, 1), B ~ (-u, -mu), C ~ (u, mu). Then P ~ (m, -1), Q ~ (-m, 1),
D ~ (a - 2(a+u)
1 + mu
 , -1),      E ~ (a + 2(a+u)
1 + mu
 , -1) .
Since |AC | = |BD |, we find that u - a = -u - a + [(2(a+u))/(1 + mu)], or a = mu2. (We can check this by equating the slopes of AC and AE.)

The slope of AE is -1/u and of AD is 1/u, so that
tanÐBAC = -(2/u)
1 - (1/u2)
 = - 2u
u2 - 1
  .
The slope of CQ is (mu - 1)/(m+u) and of BQ is (1 + mu)/(u-m), so that
tanÐBPC = tanÐBQC
= (mu - 1)(u - m) - (mu + 1)(u + m)
(u - m)(u + m) + (mu - 1)(mu + 1)
= -2(m2 u + u)
u2 - m2 + m2 u2 - 1
 = -2(m2 + 1)u
(1 + m2)(u2 - 1)
 = -2u
u2 - 1
  .
The result follows.

13.
Third solution. [M. Boase] Let XAY be drawn parallel to DE.
Since M is the midpoint of BC, the distance from M to DE is the average of the distances from B and C to DE. Similarly, the distance from M to XY is the average of the distances from B and C to XY. The distance of B (resp. C) to DE equals the distance of C (resp. B) to XY. Hence, M is equidistant from DE and XY. If PM produced meets XY in Q, then PM = MQ and so ÐBQC = ÐBPC.
Select R on MQ (possibly produced) so that ÐBAC = ÐBRC. Since DADE ||| DRBC, ÐRBC = ÐRCB = ÐADE. Since BARC is a concyclic quadrilateral, ÐBAR = 180° - ÐRCB = 180° - ÐADE = 180°- ÐXAD = ÐBAQ from which it follows that R = Q and so ÐBPC = ÐBQC = ÐBRC = ÐBAC.


13.
Fourth solution. [Jimmy Chui] Set coordinates: A ~ (0, (m+n)b), B ~ (-ma, nb), C ~ (na, mb) D ~ (-(m+n)a, 0) and E ~ ((m+n)a, 0) where m = |AB |, n = |AC | and a2 + b2 = 1. Then the line BC has the equation
m-n
a
 x - m+n
b
 y + m2 + n2 = 0
and the right bisector of BC has equation
m+n
b
 x + m-n
a
 y + (a2 - b2)(m2 - n2)
2ab
 = 0  .
Thus
P ~ æ
ç
è 		(b2 - a2)(m - n)
2a
 , 0 ö
÷
ø 		 .
Now
|BC |2 = m2 + n2 + 2mn(a2 - b2)
and
|BP |2 = m2 + n2 + 2mn(a2 - b2)
4a2
so that |BC |/ |BP | = 2a. Also |DE |/ |AD | = 2(m+n)a/(m+n) = 2a so that DBPC is similar to DADE and the result follows.

13.
Fifth solution. Determine points L and N on DE such that BL || AE and LN = NE. Now
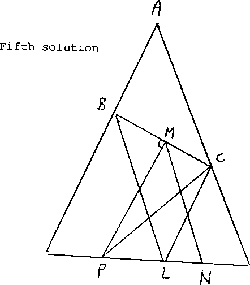
LE
LD
 = AB
BD
 = CE
CA
so that CL || AD and CL:AD = CE:AE. Since AD = DE, CL = CE and so CN ^LE. Consider the trapezoid CBLE. The line MN joins the midpoints of the nonparallel opposite sides and so MN || BL. MPNC is a quadrilateral with right angles at M and N, and so is concyclic. Hence
ÐBPC = 2ÐMPC = 2ÐMNC = 2ÐNCE = ÐLCE = ÐBAC  .


13.
Sixth solution. [C. So] Let F, N, G be the feet of the perpendiculars dropped from B, M, C respectively to DE. Note that FN = NG, so that MF = MG. Let ÐADE = ÐAED = q, |AB | = c, |AC | = b and h be the altitude of DADE. Then
|MN | = 1
2
 [ |BF |+ |CG |] = 1
2
 (b + c)sinq = h
2
and
|DF | = b cosq ,    |GE | = c cosq ,   |DE | = 2(b + c)cosq  .
Hence |FG | = |DE |- |DF |- |GE | = 1/2 |DE |. Since DADE and DMFG are isosceles triangles with heights and beses in proportion, they are similar so that ÐMFG = ÐADE = q. Since ÐBFP = ÐBMG = 90°, the quadrilateral BFPM is concyclic and so ÐCBP = ÐMFP = q (we are supposing that the configuration is labelled so P lies between F and E). Hence DADE is similar to DPCB and so ÐBPC = ÐBAC.

13.
Seventh solution. [A. Chan] Let ÐADE = ÐAED = q, so ÐBAC = 180° - 2q. Suppose that ÐACB = f, ÐCPE = s and ÐBCP = r. By the Law of Sines for triangles ABC and PCE, we find that
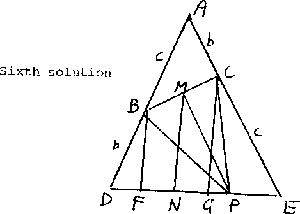
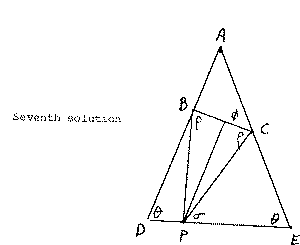
2 |PC |cosr
sin2q
 = |AB |
sinf
whence
sins
sinq
 = |CE |
|PC|
 = |AB |
|PC |
 = 2 cosrsinf
sin2q
and
sinscosq = sinfcosr  .
Therefore
sin(q+ s) + sin(s- q) = sin(f+ r) + sin(f- r).
Since q+ s = f+ r, sin(s- q) = sin(f- r). Either (s- q) + (f- r) = ±180° or s- q = f- r. In the first case, since q+ s = f+ r, |s- r| = 90°, which is false.

Hence s- q = f- r, so, with q+ s = f+ r, we have that
2 q = q+ (r+ s- f) = q+(r+ r- s) = 2r
and the result follows.

14.

14.
(a) First solution. Since c = a + d - b, we have that
bc - ad = b(a + d - b) - ad = (a - b)b - (a - b)d = (a - b)(b - d) > 0  .

(a) Second solution. Let a + d = b + c = u. Then
bc - ad = b(u - b) - (u - d)d = u(b - d) - (b2 - d2) = (b - d)(u - b - d) .
Now u = b + c > b + d, so that u - b - d > 0 as well as b - d > 0. Hence bc - ad > 0 as desired.

(a) Third solution. Let x = a - b > 0. Since a - b = c - d, we have that a = b + x and d = c - x. Hence
bc - ad = bc - (b + x)(c - x) = bx - cx + x2 = x2 + x(b - c) > 0 .

(a) Fourth solution. Since Öa > Öb > Öc > Öd, Öa - Öd > Öb - Öc. Squaring and using a + d = b + c yields 2Ö[bc] > 2Ö[ad], whence the result.
14.
(b) First solution. Since all variables represent integers,
aq - bp > 0, br - as > 0 Þ aq - bp ³ 1,br - as ³ 1 .
Therefore
b = b(qr - ps) = q(br - as) + s(aq - bp) ³ q + s .
15.

15.
(a) First solution. Since F0 = F2 - F1 = 0, the result holds for n = 0. Since F-1 = F1 - F0 = 1, the result holds for n = 1. Suppose that we have established the result for n = 0, 1, 2, ¼r. Then
F-(r+1) = F-r-1 = F-r+1 - F-r = (-1)r Fr-1- (-1)r+1 Fr = (-1)r+2(Fr-1 + Fr) = (-1)r+2Fr+1 .
The result follows by induction.

15.
(b) First solution. The result holds for n = 0, n = 1 and n = 2. Suppose that it holds for n = 0, 1, 2, ¼,r. Then
tr+1 = tr + tr-1 = (Fr + Fr-1)t+ (Fr-1 + Fr-2) = Fr+1t+ Fr t .
This establishes the result for positive values of n. Now t-1 = t- 1 = F-1t+ F-2, so the result holds for n = -1. Suppose that we have established the result for n = 0, -1, -2, ¼, -r. Then
t-(r+1) = t-(r-1) - t-r = (F-(r-1) - F-r)t+ (F-r - F-(r+1)) = F-(r+1)t+ F-(r+2) .

15.
(b) Second solution. The result holds for n = 1. Suppose that it holds for n = r ³ 0. Then
tr+1 = tr ·t = (Fr t+ Fr-1) t = Fr t2 + Fr-1t
= (Fr + Fr-1)t+ Fr = Fr+1 t+ Fr   .
Now consider nonpositive values of n. We have that t0 = 1, t-1 = t- 1, t-2 = 1 - t-1 = 2 - t. Suppose that we have shown for r ³ 0 that t-r = F-r t+ F-r-1. Then
t-(r+1) = t-1 t-r = F-r + F-r-1(t- 1) = F-r-1 t+ (F-r - F-r-1)
= F-r-1t+ F-r-2 = F-(r+1)t+ F-(r+1)-1  .
By induction, it follows that the result holds for both positive and negative values of n.

15.
(c) First solution. Let Gn = Fn Fn+1. Then
Gn+3 + Gn
= Fn+4Fn+3 + Fn+1Fn
= (Fn+3 + Fn+2)(Fn+2 + Fn+1) +(Fn+3 - Fn+2)(Fn+2 - Fn+1)
= 2(Fn+3 Fn+2 + Fn+2 Fn+1) = 2(Gn+2 + Gn+1) .

Let Gn = Fn+1Fn-1. Then
Gn+3 + Gn
= Fn+4Fn+2 + Fn+1Fn-1
= (Fn+3 + Fn+2)(Fn+1 + Fn) +(Fn+3 - Fn+2)(Fn+1 - Fn)
= 2(Fn+3 Fn+1 + Fn+2 Fn) = 2(Gn+2 + Gn+1) .

Let Gn = Fn2. Then
Gn+3 + Gn
= Fn+32 + Fn2 = (Fn+2 + Fn+1)2 + (Fn+2 - Fn+1)2
= Fn+22 + 2Fn+2Fn+1 + Fn+12+ Fn+22 - 2Fn+2Fn+1 + Fn+12 = 2(Gn+2 + Gn+1) .

Comments. Since Fn2 = Fn Fn-1 + Fn Fn-2, the third result of (c) can be obtained from the first two. J. Chui observed that, more generally, we can take Gn = Fn+uFn+v where u and v are integers. Then
Gn+3 + Gn
- 2(Gn+1 + Gn+2)
= (Fn+3+uFn+3+v + Fn+uFn+v) - 2(Fn+2+uFn+2+v + Fn+1+uFn+1+v)
= (2Fn+1+u + Fn+u)(2Fn+1+v + Fn+v) + Fn+uFn+v
          - 2(Fn+1+u + Fn+u)(Fn+1+v + Fn+v) - 2Fn+1+uFn+1+v
= 0  ,
so that Gn+3 + Gn = 2(Gn+2 + Gn+1).

16.

16.
(a) First solution. Let
l = cosb
cosa
     and     m = sinb
sina
  .
Since l-1 + m-1 = -1, we have that l+ m = -lm. Now
1 = cos2 b+ sin2 b = l2 cos2 a+ m2 sin2 a = l2 + (m2 - l2)sin2a = l2 - (m- l)lmsin2 a .
Hence
cos3 b
cosa
 + sin3 b
sina
= l3 cos2 a+ m3 sin2 a
= l(l2 cos2 a+ m2 sin2 a) + (m- l)m2 sin2 a
= l+ (m- l)m2 sin2 a
= 1
l
 [l2 + (l2 - 1)m]
= 1
l
 [l2 + l2 m+ l+ lm
= l+ lm+ 1 + m = 1   .

16.
(a) Second solution. [M. Boase]
cosa
cosb
 + sina
sinb
 = -1 Þ
sin(a+ b) + sinbcosb = 0 .       (*)
Therefore
cos3 b
cosa
 + sin3 b
sina
= cosb(1 - sin2 b)
cosa
 + sinb(1 - cos2 b)
sina
= cosb
cosa
 + sinb
sina
 - sinbcosb æ
ç
è 		sinb
cosa
 + cosb
sina
 ö
÷
ø
= sin(a+ b)
cosasina
 - cosbsinb(cos(a- b))
cosasina
= -2 sinbcosb+ 2 sin(a+ b) cos(a- b)
2 sinacosa
    using  (*)
= -2 sinbcosb+ [sin2a+ sin2b]
sin2a
 = 1
since 2 sinbcosb = sin2b.

16.
(a) Third solution. [A. Birka] Let cosa = x and cosb = y. Then
sina
sinb
 = ±   æ
 ú
Ö
1 - x2
1 - y2
 
   .
Since
x
y
 + 1 = -±   æ
 ú
Ö
1 - x2
1 - y2
 
   .
then
(x2 + 2xy + y2)(1 - y2) = y2(1 - x2)  ,
whence
x2 + 2xy = 2xy3 + y4  .
Thus,
cos3 b
cosa
 + sin3 b
sina
= y3
x
 ±(1 - y2)   æ
 ú
Ö
1 - y2
1 - x2
 
= y3
x
 - (1 - y2)y
x + y
 = y4 + 2xy3 - xy
x(x+y)
= x2 + xy
x(x + y)
 = 1  .

16.
(a) Fourth solution. [J. Chui] Note that the given equation implies that sin2b = -2sin(a+ b) and that the numerator of
cosa
cosb
 + sina
sinb
 + cos3 b
cosa
 + sin3 b
sina
is one quarter of
4[cos2 asinasinb
+ sin2 acosacosb+cos4 bsinasinb+ sin4 bcosacosb]
= 4[cos2 asinasinb+ sin2 acosacosb+ (cos2 b- cos2 bsin2 b)sinasinb
             + (sin2 b- sin2 bcos2 b)cosacosb]
= (4cos2 a+ 4cos2 b- sin2 2b)sinasinb+ (4sin2 a+ 4sin2 b- sin2 2b)cosacosb
= 2sin2acosasinb+ 2sin2bcosbsina+ 2sin2asinacosb+2sin2bcosasinb
           - sin2 2b(cosacosb+ sinasinb)
= 2(sin2a+ sin2b) sin(a+ b)- sin2 2bcos(a- b)
= 2sin(a+ b) [sin2a+ sin2b-2sin(a+ b)cos(a- b)] = 0   ,
since
sin2a+ sin2b = sin(
a+ b
 
 +
a- b
 
 )+ sin(
a+ b
 
 -
a- b
 
 ) .

16.
(a) Fifth solution. [A. Tang] From the given equation, we have that
sin(a+ b) = -sinbcosb  ,
cosb
cosa
 = -sinb
sina+ sinb
   ,
and
sinb
sina
 = -cosb
cosa+ cosb
   .
Hence
cos3 b
cosa
 + sin3 b
sina
= cos2b é
ê
ë 		-sinb
sina+ sinb
 ù
ú
û 		+ sin2 b é
ê
ë 		-cosb
cosa+ cosb
 ù
ú
û
= - sinbcosb[cosacosb+sinasinb+ 1]
4 sin 1
2
 (a+ b) cos 1
2
 (a-b) cos 1
2
 (a+ b) cos 1
2
 (a- b)
= sin(a+ b) [cos(a- b) + 1]
[2 sin 1
2
 (a+ b) cos 1
2
 (a+ b)][2 cos2 1
2
 (a- b)]
 = 1  .

16.
(a) Sixth solution. [D. Arthur] The given equations yield 2 sin(a+ b) = -sin2b, cosasinb = -cosb(sina+ sinb) and sinacosb = -sinb(cosa+ cosb). Hence
cos3 b
cosa
 + sin3 b
sina
= cos2 b(cosbsina) + sin2 b(sinbcosa)
cosasina
= - cos2 bsinb(cosa+ cosb) -sin2 bcosb(sina+ sinb)
cosasina
= - cosbsinb(cosacosb+ cos2 b+ sinasinb+ sin2 b)
cosasina
= - sin2b(1 + cos(a- b))
sin2a
= - sin2b+ 2sin(a+ b)cos(a- b)
sin2a
= - sin2b+ sin2a+ sin2b
sin2a
 = 1  .

16.
(b) First solution. The given equation is equivalent to 2 sin(a+ b) + sin2b = 0. Try b = -45° so that sin(a- 45°) = 1/2. We take a = 75°. Now
sin75° = sin(45° + 30°) = 1
Ö2
 æ
ç
è 		Ö3 + 1
2
 ö
÷
ø
and
cos75° = cos(45° + 30°) = 1
Ö2
 æ
ç
è 		Ö3 - 1
2
 ö
÷
ø 		  .
It is straightforward to check that both equations hold.

17.

17.
First solution. Taking x = 1, 2, 3, ¼ yields the respective sequences
{ 1, 1, 0, -1, -1, 0, ¼} ,   { 2, 8, 30, 112, 418, 1560, ¼} ,   { 3, 27, 240, 2133, ¼} .
In each case, we find that
Pn+1(x) = x2 Pn (x) - Pn-1(x)       (1)
for n = 2, 3, ¼. If we can establish (1) in general, it will follow that all the functions Pn are polynomials.

From the definition of Pn, we find that
Pn+1 + Pn-1 = Pn (Pn2 - Pn+1Pn-1)  .
Therefore, it suffices to establish that Pn2 - Pn+1Pn-1 = x2 for each n. Now, for n ³ 2,
[Pn+12 - Pn+2Pn]
-[Pn2 - Pn+1Pn-1] = Pn+1(Pn+1 + Pn-1) - Pn (Pn+2 + Pn)
= Pn+1Pn(Pn2 - Pn+1Pn-1) - Pn Pn+1(Pn+12 - Pn+2Pn)
= -Pn+1Pn [(Pn+12 - Pn+2Pn) -(Pn2 - Pn+1Pn-1)]  ,
so that either Pn+1(x)Pn(x) + 1 º 0 or Pn+12 - Pn+2Pn = Pn2 - Pn+1Pn-1. The first identity is precluded by the case x = 1, where it is false. Hence
Pn+12 - Pn+2Pn = Pn2 - Pn+1Pn-1
for n = 2, 3, ¼. Since P2 2 (x) - P3(x)P1(x) = x2, the result follows.

17.
Second solution. [By inspection, we make the conjecture that Pn (x) = x2 Pn-1(x) - Pn-2. Rather than prove this directly from the rather awkward condition on Pn, we go through the back door.] Define the sequence { Qn } for n = 0, 1, 2, ¼ by
Q0(x) = 0  ,        Q1(x) = x ,       Qn+1 = x2 Qn (x) - Qn-1(x)
for n ³ 1. It is clear that Qn (x) is a polynomial of degree 2n - 1 for n = 1, 2, ¼. We show that Pn(x) = Qn (x) for each n.

Lemma: Qn2 (x) - Qn+1Qn-1 = x2 for n ³ 1.
Proof: This result holds for n = 1. Assume that it holds for n = k-1 ³ 1. Then
Qk2(x) - Qk+1(x)Qk-1(x)
= Qk2 (x) - (x2 Qk (x) - Qk-1(x))Qk-1(x)
= Qk (x) (Qk(x) - x2 Qk-1(x)) + Qk-12 (x)
= -Qk (x) Qk-2 (x) + Qk-12 (x) = x2 .     QED

From the lemma, we find that
Qn+1 (x)
+ Qn-1(x) + Qn+1(x) Qn(x) Qn-1(x)
= x2 Qn (x) + Qn+1(x) Qn (x) Qn-1(x) = Qn (x)(x2 + Qn+1 (x) Qn-1(x)) = Qn3(x)
Þ Qn+1(x) = Qn3(x) - Qn-1(x)
1 + Qn (x) Qn-1(x)
       (n = 1, 2, ¼) .
We know that Q1 (x) = P1 (x) and Q2 (x) = P2 (x). Suppose that Qn (x) = Pn (x) for n = 1, 2, ¼, k. Then
Qk+1 (x) = Qk3 (x) - Qk-1(x)
1 + Qk (x) Qk-1(x)
 = Pk3 (x) - Pk-1(x)
1 + Pk (x) Pk-1(x)
 = Pk+1(x)
from the definition of Pk+1. The result follows.

Comment: It can also be established that Pn+12 + Pn2 = (1 + Pn Pn+1)x2 for each n ³ 0.
17.
Third solution. [I. Panayotov] First note that the sequence { Pn (x) } is defined for all values of x, i.e., the denominator 1 + Pn-1(x)Pn(x) never vanishes for n and x. Suppose otherwise, and let n be the least number for which there exists u for which 1 + Pn-1(u)Pn (u) = 0. Then n ³ 3 and
-1 = Pn-1(u) Pn(u) = Pn-1(u)4 - Pn-1(u)Pn-2(u)
1 + Pn-1(u)Pn-2(u)
which implies that Pn-1(u)4 = -1, a contradiction.

We now prove by induction that Pn+1 = x2 Pn - Pn-1. Suppose that Pk = x2 Pk-1 - Pk-2 for 3 £ k £ n, so that in particular we know that Pk is a polynomial for 1 £ k £ n. Substituting for Pk yields
Pk-13(x) = Pk-1(x)[x2 + x2 Pk-1(x)Pk-2(x)- Pk-22(x)]
for all x. If Pk-1(x) ¹ 0, then
Pk-12 (x) = x2 + x2Pk-1Pk-2(x) - Pk-22(x) .
Both sides of this equation are polynomials and so continuous functions of x. Since the roots of Pk-1 constitute a finite discreet set, this equation holds when x is one of the roots as well. Now
Pn+1
= Pn3 - Pn-1
1 + Pn Pn-1
 = Pn (x2 Pn-1 - Pn-2)2 - Pn-1
1 + Pn Pn-1
= Pn (x4 Pn-12 - x2 Pn-1Pn-2 + x2 - Pn-12) - Pn-1
1 + Pn Pn-1
= Pn (x2 Pn Pn-1 + x2 - Pn-12) - Pn-1
1 + PnPn-1
          since   x2 Pn-1 - Pn-2 = Pn
= (x2 Pn - Pn-1)(1 + Pn Pn-1)
1 + Pn Pn-1
 = x2 Pn - Pn-1  .
The result follows.

18.

18.
First solution. Suppose that the points in the plane are coloured with three colours. Select any point P.
Consider the diagrammed configuration, in which all segments have length 1. If P, Q, R are all coloured differently, then either the result holds or S must have the same colour as P. If P, U, V are all coloured differently, then either the result holds or W must have the same colour as P. Hence, either one of the triangles PQR and PUV has two vertices the same colour, or else S and W must be coloured the same.
18.
Second solution. Suppose, if possible, the planar points can be coloured without two points unit distance apart being coloured the same. Then if A and B are distant Ö3 apart, then there are distinct points C and D such that ACD and BCD are equilateral triangles (ABCD is a rhombus). Since A and B must be coloured differently from the two colours of C and D, A and B must have the same colour. Hence, if O is any point in the plane, every point on the circle of radius Ö3 consists of points coloured the same as O. But there are two points on this circle unit distant apart, and we get a contradiction of our initial assumption.
18.
Third solution. Suppose we can colour the points of the plane with three colours, red, blue and yellow so that the result fails. We show that three collinear points at unit distance are coloured with three different colours. Let P, Q, R be three such points, and embed P, Q, R in the hexagon ABPCDR as indicated with all indicated segments of unit length.
If, say, Q is red, B and A must be coloured differently, as are A and R, R and D, D and C, C and P, P and B. Thus, B, R, C, are one colour, say, blue, and A, D, P the other, say yellow. The preliminary result follows.
Now consider any isosceles triangle UVW with |UV | = |UW | = 3 and |VW | = 2. It follows from the preliminary result that U and V must have the same colour, as do U and W. But V and W cannot have the same colour and we reach a contradiction.
18.
Fourth solution. [D. Arthur] Suppose that the result is false. Let A, B be two points with |AB | = 3. Within the segment AB select PQ with |AP | = |PQ | = |QB | = 1, and suppose that R and S are points on the same side of AB with DRAP and DSPQ equilateral. Then |RS | = 1. Suppose if possible that A and Q have the same colour. Then P must have a second colour and R and S the third, leading to a contradiction. Hence A must be coloured differently from both P and Q. Similarly B must be coloured differently from both P and Q. Since P and Q are coloured differently, A and B must have the same colour.
Now consider a trapezoid ABCD with |CB | = |AB| = |AD | = 3 and |CD | = 1. By the foregoing observation, C, A, B, D must have the same colour. But this yields a contradiction. The result follows.
© Société mathématique du Canada, 2025 : https://smc.math.ca/