1998-1999 Olympiad Correspondence Problems

Set 4

19.

The following statics problems involving vectors was given and two separate solutions provided. Determine whether either of them is correct and explain the discrepancy between the answers.

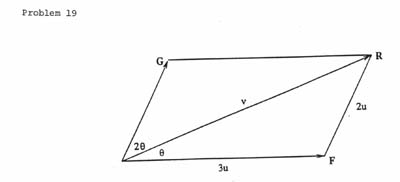
Problem. A force R of magnitude 200 N (Newtons) is the resultant of two forces F and G for which 2 |F | = 3 |G | and the angle between the resultant and G is twice the angle between the resultant and F. Determine the magnitudes of F and G.

Both solutions use the parallelogram representation of the vectors as illustrated, where 3u = |F |, 2u = |G| and v = |R | = 200. From the Law of Sines, we have that

sin2q 3 = sinq 2

whence cosq = 3/4, cos2q = 1/8 and cos3q = 4cos³ q- 3cosq = -9/16. >From here, there are two ways to proceed:

(i) From the Law of Cosines, we find that

v2 = 4u2 + 9u2 - 12u2 cos(180° - 3q) = 13u2 + 12u2 cos3q = 25u2 4

so that 200 = ⁵/₂u, u = 80, |F | = 240 and |G | = 160.

(ii) From the Law of Cosines, we find that

4u2 = 9u2 + v2 - 6uv cosq = 9u2 + 2002 - 900u

so that

0 = 5(u2 - 180u + 8000) = 5(u - 80)(u - 100) .

Hence, u = 80, |F | = 240, |G| = 160 or u = 100, |F | = 300, |G | = 200.

Why does method (i) lead to one solution while method (ii) yields two? QED

View solution

20.

Using a pair of compasses with a fixed radius exceeding half the length of a line segment AB, it is possible to determine a point C for which the triangle ABC is equilateral. Here is how it is done.

With centres A and B construct circles using the compasses and let P be one of the two points of intersection of these circles. Draw the circle with centre P, and let it intersect the circle of centre A in Q and the circle of centre B in R. There are different possible configurations, but we will select one so that QR is parallel to AB. Now construct, using the compasses again, circles of centres Q and R. These will intersect in P and a second point C. Prove that triangle ABC is equilateral.

View solution

21.

In the following problem, we will begin by making some empirical observations. Your task will be to formulate some general results exemplified by them and provide proofs. You may observe some other general results not really pointed to below; if so, formulate and justify these.

The numbers 1, 2, 3, ¼ are placed in a triangular array and certain observations concerning row sums are made as indicated below:

The odd row sums of this array are 1, 35, 189, 559, ¼ and their running totals are 1 = 1², 36 = 2² ·3² = (1+2+3)², 225 = 3² ·5² = (1+2+3+4+5)², 784 = 4² ·7² = (1+2+3+4+5+6+7)², ¼, You will notice that the square roots are the sum of odd sums of consecutive integers. Even sums are not to be left out. The even row sums in the array are 9, 91, 341, ¼ and their running totals are 9 = 1² ·3² = (1+2)², 100 = 2² ·5² = (1+2+3+4)², 441 = 3² ·7² = (1+2+3+4+5+6)², ¼.

We can continue in this vein. Writing the triangular array with 1, 4, 7, 10, ¼ numbers in the consecutive rows, we find the running totals of the odd sums to be 1, 64 = 8² = 2² ·4², 441 = 21² = 3² ·7² and so on. With 1, 5, 9, 13, ¼ numbers in the consecutive rows, the running totals of the odd sums are 1, 100 = 10² = 2² ·5², 729 = 27² = 3²·7².

View solution

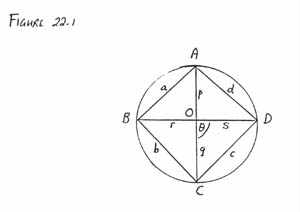
22.

The diagonals of a concyclic quadrilateral ABCD intersect in a point O. Establish the inequality

AB CD + CD AB + BC AD + AD BC £ OA OC + OC OA + OB OD + OD OB  .

View solution

23.

Let A₁, A₂, ¼, A_r be subsets of { 1, 2, ¼, n } such that no A_i contains another. Suppose that A_i has a_i elements (1 £ i £ r). Prove that

å æ ç è n ai ö ÷ ø -1   £ 1 .

View solution

24.

Without recourse to a calculator or a computer, give an argument that 512³ + 675³ + 720³ is composite. View solution

---

Problem 19.

19.

First solution. Method (i) leads to the equation 0 = (5u - 2v)(5u + 2v) while (ii) leads to 4u² = 9u² + v² - 9uv/2 or 0 = (5u - 2v)(2u - v). Let us examine closely the second answer that is provided by (ii). In this case, the triangle formed by the two vectors and their resultant is isosceles with sides of magnitudes 3u, 2u and 2u with the base angle equal to q and the apex angle equal to 180^° - 2q. In this configuration, cosq is indeed 3/4, but the apex angle is not 2q as specified in the statement of the problem. Indeed, method (i) made use of the angle between R and G. However in method (ii) the result of the sine law remained valid with 180^° - 2q in place of 2q but the cosine law did not make use of the angle between R and G. So it is not surprising that the second method leads to a spurious possibility.

---

Problem 20.

20.

There are various configurations, and we give the solution for one of these. The solutions for the other are similar.

20.

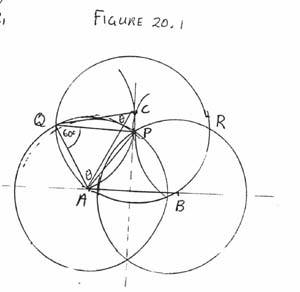
First solution. See Figure 20.1. We have that AP = AQ = QP = QC. Let ÐQAC = ÐQCA = q, so that ÐAQC = 180^°- 2q. Then ÐPQC = ÐAQC - 60^° = 120^° - 2q, so that ÐQCP = ÐQPC = 30^° + q. Thus, ÐACP = 30^°. Since CP ^AB, ÐCAB = 60^°. Similarly, ÐCBA = 60^° and so DABC is equilateral.

20.

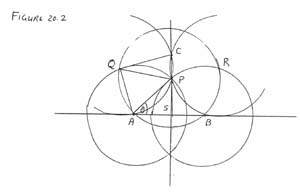
Second solution. See Figure 20.2.Consider the reflection in the right bisector of AB. It interchanges circles with centres A and B, and hence fixes their intersection points, in particular P. This reflection also carries the circle with centre P to itself. Hence the point C is fixed by the reflection. It follows that P and C are on the right bisector of AB.

Suppose that PC intersects AB in S. Let ÐSAP = q. Then ÐAPB = 180^° - 2q. Also

ÐQPC = 180° - ÐAPQ - ÐAPS = 180° - 60° - (90° - q) = 30° + q

whence

ÐPQC = 180° - 2(30° + q) = 120°- 2q

and

ÐAQC = 60° + ÐPQC = 180° - 2q .

Hence DAQC º DAPB (SAS) so that AC = AB and the result follows.

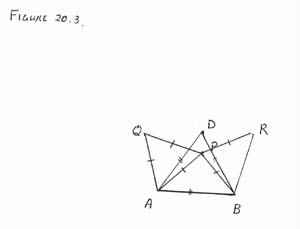
Third solution. See Figure 20.3. A 60^° clockwise rotation about A followed by a 60^° clockwise rotation about B takes A ® A ® D and Q ® P ®R, where D is the third vertex of an equilateral triangle with side AB. Hence AQ ® DR so that |DR | = |AQ |, the radius of the circle.

Similarly, the composition of two counterclockwise rotations with respective centres B and A takes B ® B ®D and R ® P ® Q, so that |DQ | = |BR |, the radius of the circle. Hence D is a point of intersection of the circles with centres Q and R. When the radius is not equal to |AB |, this will be distinct from P, so that D = C, and the result follows.

---

Problem 21.

21.

First solution. Consider the triangular array in which the consecutive positive integers are written in rows with only the number 1 in the top row and with k ³ 0 more elements in each row than the previous one. For r ³ 1, the rth row has (r-1)k + 1 elements beginning with ((r-1) || 2)k + r and ending with (r || 2)k + r. The sum of the numbers in the rth row is

1 2 [(r-1)k + 1] é ê ë æ ç è æ ç è r-1 2 ö ÷ ø + æ ç è r 2 ö ÷ ø ö ÷ ø k + 2r ù ú û = 1 2 [(r-1)k + 1][(r-1)2k + 2r] = 1 2 [ (r-1)3 k2 + (3r2 - 4r + 1)k + 2r]  .

When r = 2s - 1, this sum is

4(s-1)3 k2 + (6s2 - 10s + 4)k + (2s - 1)

and the sum of the first m odd-numbered rows is the sum of these terms over 1 £ s £ m, namely

[m(m-1)k]2 + 2m2(m-1)k + m2 = [m((m-1)k + 1)]2 .

When k = 0, the sum of the elements in the sth odd-numbered row is 2s - 1 and the sum of the elments in the first m odd-numbered rows is m², the sum of the first m odd integers.

When k = 1, the sum of the elements in the sth odd-numbered row is

4(s-1)3 + (6s2 - 10s + 4) + (2s - 1) = 4s3 - 6s2 + 4s - 1 = s4 - (s-1)4 = [s2 - (s-1)2][s2 + (s-1)2] = [(s-1) + s][(s-1)2 + s2]

and the sum of all the elements in the first m odd-numbered rows is m⁴.

When k = 2, the sum of the elements in the first m odd-numbered rows is

[m(2m - 1)]2 = [(1/2)(2m)(2m-1)]2 = [1 + 2 + ¼+ 2m-1   ]2  .

When r = 2s, the sum of the elements in the rth row is

1 2 [(2s - 1)3 k2 + (12s2 - 8s + 1)k + 4s] .

For k = 0, this sum is 2s. When k = 1, the sum is 4s³ + s = s[1 + (2s)²] and the sum of all the elements in the first m even-numbered rows is

m2 (m+1)2 + 1 2 m(m+1) = æ ç è m+1 2 ö ÷ ø [m2 + (m+1)2] = [1 + 2 + ¼+ m][m2 + (m+1)2]  .

For k = 2, the sum of the numbers in the sth even-numbered row is

2(2s - 1)3 + (12s2 - 8s + 1) + 2s = 16s3 - 12s2 + 6s - 1 = (2s - 1)3 + (2s)3

and the sum of all the elements in the first m even-numbered rows is

m å s = 1  [(2s - 1)3 + (2s)3] = 2m å r = 1  r3 = [1 + 2 + ¼+ 2m]2 .

---

Problem 22.

22.

First solution. Let the points and lengths be as labelled in the diagram, and let q = ÐAOB, a = ÐBAD, b = ÐABC. Then ÐBCD = 180^° - a and ÐCDA = 180^° - b. Then, where [ ¼] denotes area,

2[ABC] = ab sinb = (p + q)rsinq

2[ACD] = cd sinb = (p + q)s sinq

so that r/s = (ab)/(cd). Similarly p/q = (ad)/(bc). Hence

p q + r s = a c æ ç è d b + b d ö ÷ ø ³ 2 a c

p q + s r = d b æ ç è a c + c a ö ÷ ø ³ 2 d b

q p + r s = b d æ ç è c a + a c ö ÷ ø ³ 2 b d

q p + s r = c a æ ç è b d + d b ö ÷ ø ³ 2 c a

and the result follows.

Second solution. From similar triangles, we find that a/c = r/q = p/s, b/d = r/p = q/s, so that pq = rs. Then

æ ç è p q + q p + r s + s r ö ÷ ø - æ ç è a c + c a + b d + d b ö ÷ ø = æ ç è p q + q p + r s + s r ö ÷ ø - æ ç è r q + s p + q s + p r ö ÷ ø = p2 + q2 - pr - qs pq + r2 + s2 - qr - ps rs  .

Since pq = rs, this is a fraction over a common denominator with numerator

p2 + q2 + r2 + s2 - pr - qs - rq - sp = 1 2 [ (p - r)2 + (q - s)2 + (q - r)2 +(s - p)2] ,

which is nonnegative. The result follows.

Third solution. Begin as in the second solution. Then

a c + b d + c a + b b = r q + q s + s p + p r = pr + qs pq + rq + sp rs = pr + qs + rq + sp pq £   ______________ Öp2 + q2 + r2 + s2     ______________ Ör2 + s2 + q2 + p2   pq = p2 + q2 + r2 + s2 pq = p2 + q2 pq + r2 + s2 rs = p q + q p + r s + s r  ,

from the Cauchy-Schwarz Inequality.

---

Problem 23.

23.

First solution. There are n! arrangements of the first n natural numbers. Suppose that a_i = k; consider the arrangements { x₁, x₂, ¼, x_n } where A_i = { x₁, x₂, ¼, x_k } (i.e., the first a_i numbers constitute the set A_i). There are k! possible ways of ordering the first k numbers and (n-k)! ways of ordering the remaining numbers so that there are a_i! (n - a_i)! arrangements of this type. Let i ¹ j. No arrangement { x₁, x₂, ¼, x_n } can at the same time have its first a_i elements coincide with A_i and its first a_j elements coincide with a_j, since neither of A_i and A_j is contained in the other. Hence a_i! (n - a_i)! arrangements corresponding to A_i are distinct from the a_j! (n - a_j)! arrangements corresponding to A_j. It follows that

n å i = 1  ai! (n - ai)! £ n!

and the result obtains.

---

Problem 24.

24.

First solution. Observe that 512 = 2⁹, 675 = 3³·5² and 720 = 2⁴ ·3² ·5, so that 2 ·720² = 3 ·512 ·675. We now use the identity

x3 + y3 + z3 = x3 + y3 - z3 + 3xyz = (x + y - z)(x2 + y2 + z2 - xy + xz + yz)

which is valid when 2z² = 3xy to obtain that

5123 + 6753 + 7203 = (512 + 675 - 720)(5122 + 6752 + 7202 - 512·675+ 512 ·720 + 675 ·720) .

Thus, 467 = 512 + 675 - 720 is a factor of the sum of cubes.

24.

Second solution. [P. LeVan]

5123 + 6753 + 7203 = 5123 + 453 [153 + 163] = 5123 + 453 [(16 - 1)3 + 163 ] = 5123 - 453 + 453 ·16 [2 ·162 - 3 ·16 + 3] = (512 - 45)(5122 + 512 ·45 + 452) + 453 ·16[512 - 3 ·15] = 467[5122 + 512 ·45 + 452] + 453 ·16 [467] = 467 [5122 + 512 ·45 + 452 + 453 ·16]

so that 467 is a factor of the sum of the cubes.

24.

Third solution. [D. Pritchard] We have the identity

(a9)3 + (b3 c2)3 + (a4 b2 c3)3 = a27 + b9 c6 + a12 b6 c3

= (a9 + b3 c2 - a4 b2 c)(a18 - a9 b3 c2 + b6 c4+ a13 b2 c + a4 b5 c3 + a8 b4 c2) + (2b - 3a)a12 b5 c3 .

Now take (a, b, c) = (2, 3, 5) to yield the desired result, one factor being 467.

24.

Fourth solution. [D. Arthur] Writing 512 = ¹/₂(x + y), 675 = ¹/₂(x + z) and 720 = ¹/₂(y + z) yields (x, y, z) = (467, 557, 883). Modulo 467, we find that

5123 + 6753 + 7203 º 8-1(2y3 + 2z3 + 3y2z + 3yz2) = 8-1(y + z)(2y2 + 2z2 + yz)  .

[Note that 8^-1 represents a number a for which 8a º 1 (mod 467).] Now y º 90 and z º -51, so that

2y2 + 2z2 + yz º 2 ×902+ 2 ×512 - 90 ×51 = 9 [4 ×450 + 2 ×289 - 510] º 9 [- 4 ×17 + 578 - 510] = 9 [-68 + 68] = 0

and so the sum of the cubes is divisible by 467.

24.

Comment. In fact,

5123 + 6753 + 7203 = 229 ×467 ×7621 .