Problem Set 6

31.

Find all continuous functions f: R ®R such that

f(x + f(y)) = f(x) + y

for every x, y Î R.

View solution

32.

Let n ³ 3 be a natural number. Prove that

1989 |nnnn - nnn   .

View solution

33.

Let n ³ 3 be a positive integer. Are there n positive integers a₁, a₂, ¼, a_n not all the same such that for each i with 3 £ i £ n we have

ai + Si = (ai, Si) + [ai, Si]  .

where S_i = a₁ + a₂ + ¼+ a_n, and where (·, ·) and [ ·, ·] represent the greatest common divisor and least common multiple respectively?

View solution

34.

Find all integers p for which there are rational numbers a and b such that the polynomial x⁵ - px - 1 has at least one root in common with the polynomial x² - ax - b.

View solution

35.

Let P be an arbitrary interior point of an equilateral triangle ABC. Prove that

|ÐPAB - ÐPAC | ³ |ÐPBC -ÐPCB |  .

(Note: This is Problem 2255 in CM+MM, September, 1997.)

View solution

36.

Let n be a positive integer and x > 0. Prove that

(1 + x)n+1 ³ (n+1)n+1 nn x  .

(Note: This is Problem 2260 in CM+MM, September, 1997.)

View solution

---

Solutions to Problem Set 6
31.

31.

First solution. Setting (x, y) = (t, 0) yields f(t + f(0)) = f(t) for all real t. Setting (x, y) = (0, t) yields f(f(t)) = f(0) + t for all real t. Hence f(f(f(t))) = f(t) for all real t, i.e., f(f(z)) = z for each z in the image of f. Let (x, y) = (f(t), -f(0)). Then

f(f(t) + f(-f(0))) = f(f(t)) - f(0) = f(0) + t - f(0) = t

so that the image of f contains every real and so f(f(t)) º t for all real t.

Taking (x, y) = (u, f(v)) yields

f(u + v) = f(u) + f(v)

since v = f(f(v)) for all real u and v. In particular, f(0) = 2f(0), so f(0) = 0 and 0 = f(-t + t) = f(-t) + f(t). By induction, it can be shown that for each integer n and each real t, f(nt) = nf(t). In particular, for each rational r/s, f(r/s) = rf(1/s) = (r/s)f(1). Since f is continuous, f(t) = f(t·1) = tf(1) for all real t. Let c = f(1). Then 1 = f(f(1)) = f(c) = cf(1) = c² so that c = ±1. Hence f(t) º t or f(t) º -t. Checking reveals that both these solutions work. (For f(t) º -t, f(x + f(y)) = -x - f(y) = f(x) + y, as required.)

31.

Second solution. Taking (x, y) = (0, 0), we find that

f(0) = 0 + f(0) Þ f(f(0)) = f(0 + f(0)) = f(0) + f(f(0))Þ f(0) = 0 .

Taking (x, y) = (0, t) yields f(f(t)) = t for all real t. Hence f(x + y) = f(x + f(f(y)) = f(x) + f(y) for all x, y, and we can complete the solution as in the First Solution.

31.

Third solution. Taking (x, y) = (0, 0) yields f(f(0)) = f(0), whence f(f(f(0))) = f(f(0)) = f(0). Taking (x, y) = (0, f(0)) yields f(f(f(0))) = 2f(0). Hence 2f(0) = f(0) so that f(0) = 0. Taking x = 0 yields f(f(y)) = y for each y. We can complete the solution as in the Second Solution.

---

32.

32.

First solution. Let N = nⁿⁿⁿ - nⁿⁿ. Since 1989 = 3² ·13 ·17,

N º 0   (mod  1989) Û N º 0   (mod    9, 13   &   17) .

We require the following facts:

(i) x^u º 0 (mod 9) whenever u ³ 2 and x º 0 (mod 3).

(ii) x⁶ º 1 (mod 9) whenever x \not º 0 (mod 3).

(iii) x^u º 0 (mod 13) whenever x º 0 (mod 13).

(iv) x¹² º 1 (mod 13) whenever x \not º 0 (mod 13), by Fermat's Little Theorem.

(v) x^u º 0 (mod 17) whenever x º 0 (mod 17).

(vi) x¹⁶ º 1 (mod 17) whenever x \not º 0 (mod 17), by FLT.

(vii) x⁴ º 1 (mod 16) whenever x = 2y + 1 is odd. (For, (2y+1)⁴ = 16y³(y+2) + 8y(3y+1) + 1 º 1 (mod 16).)

Note that

N = nnn é ê ë n(nnn - nn) - 1 ù ú û = nnn é ê ë nnn (nnn - n - 1) - 1 ù ú û  .

Modulo 17. If n º 0 (mod 17), then nⁿⁿ º 0, and so N º 0 (mod 17).

If n is even, n ³ 4, then nⁿ º 0 (mod 16), so that

nnn(nnn - n - 1) º 1(nnn - n - 1) º 1

so N º 0 (mod 17).

Suppose that n is odd. Then nⁿ º n (mod 4)

Þ nn - n = 4r  for  some  r Î N

Þ nnn - n = n4r º 1  (mod 16)

Þ nnn - n - 1 º 0  (mod 16)

Þ nnn(nnn - n - 1) º 1  (mod 17

Þ N º 0  (mod  17)  .

Hence N º 0 (mod 17) for all n ³ 3.

Modulo 13. If n º 0 (mod 13), then nⁿⁿ º 0 and N º 0 (mod 13).

Suppose that n is even. Then nⁿ º 0 (mod 4), so that nⁿⁿ - nⁿ º 0 (mod 4). Suppose that n is odd. Then n^{nn - n} - 1 º 0 (mod 16) and so nⁿⁿ - nⁿ º 0 (mod 4).

If n º 0 (mod 3), then nⁿ º 0 so nⁿ(n^{nn - n} - 1) º 0 (mod 3). If n º 1 (mod 3), then n^{nn - n} º 1 so nⁿ(n^nn-n - 1) º 0 (mod 3). If n º 2 (mod 3), then, as nⁿ - n is always even, n^nn-n º 1 so nⁿ(n^nn-n - 1) º 0 (mod 3). Hence, for all n, nⁿⁿ - nⁿ º 0 (mod 3).

It follows that nⁿⁿ - nⁿ º 0 (mod 12) for all values of n. Hence, when n is not a multiple of 13, n^{(nnn - n)} º 1 so N º 0 (mod 13).

Modulo 9. If n º 0 (mod 3), then nⁿⁿ º 0 (mod 9), so N º 0 (mod 9). Let n \not º 0 (mod 9). Since nⁿⁿ - nⁿ is divisible by 12, it is divisible by 6, and so n^{(nnn - nn)} º 1 and N º 0 (mod 9). Hence N º 0 (mod 9) for all n.

The required result follows.

---

33.

33.

First solution. Letting b_i = (a_i, S_i), we find that

[ai , Si] = ai Si (ai, Si) = ai Si bi  .

The given condition is equivalent to a_i + S_i = b_i + (a_i S_i/b_i), which is equivalent to

0 = bi2 - (ai + Si)bi + ai Si = (bi - ai)(bi - Si) .

We can achieve the condition by making a_i = (a_i, S_i) and S_i = [a_i, S_i]. Let a₁ = a₂ = 1, a_i = 2^i-2 for i ³ 3. Then

Si = 1 + i å j = 2  2j-2 = 1 + (2i-1 - 1) = 2i-1

Þ (ai, Si) = 2i-2 ,   [ai, Si] = 2i-1

for i ³ 3.

33.

Second solution. Let a_i = 1, a₂ = 2 and a_i = 3 ·2^i-3 for i ³ 3. Then

Si = 1 + 2 + 3 i-3 å j = 0  2j = 1 + 2 + 3(2i-2 - 1) = 3 ·2i-2

Þ (ai, Si) = 3 ·2i-3 ,  [ai, Si] = 3 ·2i-2

for i ³ 3.

33.

Third solution. [K. Purbhoo] Choose a₁ at will, and let a_i = S_i-1 for i ³ 2. Then S_i = S_i-1 + a_i = 2a_i, a_i + S_i = 3a_i, (a_i, S_i) = a_i and [a_i, S_i] = 2a_i for i ³ 2.

33.

Fourth solution. [K. Yeats] Let a₁ = 1, a₂ = 3 and a_n = 2^n-1 for n ³ 3. Then S_n = 2ⁿ for n ³ 2 and, for each i with 3 £ i £ n, (a_i, S_i) = 2^i-1 and [a_i, S_i] = 2ⁱ.

---

34.

34.

First solution. A common rational root must be 1 or -1, in which case the respective values of p are 0 and 2. These roots are shared with x² - 1 (a = 0, b = 1). Suppose that there is a common nonrational root r. Then r² = ar + b so that

r4 = a2 r2 + 2abr + b2 = (a3 + 2ab)r + (a2 b + b2)

whence

pr + 1 = r5 = (a3 + 2ab)r2 + (a2 b + b2)r = (a4 + 3a2 b + b2)r + b(a3 + 2ab) .

Since r is not rational,

p = a4 + 3a2 b + b2    and     1 = b(a3 + 2ab) .

Hence 2ap - 1 = 2a⁵ + 5a³ b, so that 5a³ b = 2ap - 2a⁵ - 1. Thus

1 = æ ç è -2a5 + 2ap - 1 5a3 ö ÷ ø æ ç è a3 + -4a5 + 4pa - 2 5a2 ö ÷ ø

from which we obtain that

25a5 = (-2a5 + 2pa - 1)(a5 + 4pa - 2) .

This simplifies to

a10 + 3pa6 + 11a5 - 4p2 a2 + 4pa - 1 = 0 .

This is a polynomial equation for a with integer coefficients. In order that a be rational, it must be an integer dividing 1. Hence a = ±1. If a = 1, then 1 = b(1 + 2b), whence b = ¹/₂ or b = -1. The first value does not give an integer value of p, but the second yields p = -1. In this case, the two polynomials are x² - x + 1 and x⁵ + x - 1 = (x² - x + 1)(x³ + x² - 1) with common roots -w and -w², where w is an imaginary cube root of unity. If a = -1, we get the equation 2b² + b + 1 = 0 which is satisfied by no rational value of b. Thus the possibilities are p = -1, 0, 2.

34.

Second solution. The rational root case can be handled as in the first solution. By long division, we find that

x5 - px - 1 = (x2 - ax - b)[x3 + ax2 + (a2 + b)x + (a3 + 2ab)]

+ (a4 + 3a2b + b2 - p)x + (a3b + 2ab2 - 1) .

If r is a nonrational root of the quadratic and the quintic, then its quadratic conjugate is also. So the quadratic must divide the quintic and both coefficients of the foregoing division must vanish. Hence p = a⁴ + 3a²b + b² and 1 = b(a³ + 2ab), and we can proceed as in the first solution.

---

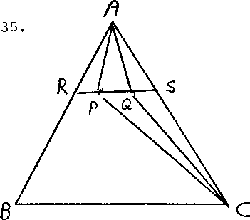
35.

35.

First solution. The result is clear if P is on the bisector of the angle at A, since both sides of the inequality are 0.

Wolog, let P be closer to AB than AC, and let Q be the image of P under reflection in the bisector of the angle A. Then

ÐPAQ = ÐPAC - ÐQAC = ÐPAC - ÐPAB

and

ÐPCQ = ÐQCB - ÐPCB = ÐPBC - ÐPCB .

Thus, it is required to show that ÐPAQ ³ ÐPCQ.

Produce PQ to meet AB in R and AC in S. Consider the reflection  with axis RS. The circumcircle C of DARS is carried to a circle C¢ with chord RS. Since ÐRCS < 60^° = ÐRAS and the angle subtended at the major arc of C¢ by RS is 60^°, the point C must lie outside of C¢. The circumcircle D of DAPQ is carried by  to a circle D¢ with chord PQ. Since D is contained in C, D¢ must be contained in C¢, so C must lie outside of D¢. Hence ÐPQC must be less than the angle subtended at the major arc of D¢ by PQ, and this angle is equal to ÐPAQ. The result follows.

---

36.

36.

First solution. By the Arithmetic-Geometric Means Inequality, we have that

1+x n+1 = n(1/n) + x n+1 ³ é ê ë æ ç è 1 n ö ÷ ø n   x ù ú û [1/(n+1)]

so that

(1 + x)n+1 (n+1)n+1 ³ x nn

and the result follows.

36.

Second solution (by calculus). Let

f(x) = nn (1 + x)n+1 - (n+1)n+1x    for  x > 0 .

Then

f¢(x) = (n+1)[nn (1 + x)n - (n+1)n] = (n+1)nn[(1 + x)n - (1 + 1 n )n ]

so that f¢(x) < 0 for 0 < x < 1/n and f¢(x) > 0 for 1/n < x. Thus f(x) attains its minimum value 0 when x = 1/n and so f(x) ³ 0 when x > 0. The result follows.

36.

Third solution. Let u = nx - 1 so that x = (1 + u)/n. Then

(1 + x)n+1 - (n+1)n+1 nn x = (1 + 1 n + u n )n+1 - (1 + 1 n )n+1(1 + u) = (1 + 1 n )n+1 + (n+1)(1 + 1 n )n u n + æ ç è n+1 2 ö ÷ ø (1 + 1 n )n-1( u n )2        + æ ç è n+1 3 ö ÷ ø (1 + 1 n )n-2( u n )3 + ¼- (1 + 1 n )n+1(1 + u) = æ ç è n+1 2 ö ÷ ø (1 + 1 n )n-1( u n )2+ æ ç è n+1 3 ö ÷ ø (1 + 1 n )n-2( u n )3 + ¼ .

This is clearly nonnegative when u ³ 0. Suppose that -1 < u < 0. For 1 £ k £ n/2, we have that

æ ç è n+1 2k ö ÷ ø (1 + 1 n )n-2k+1( u n )2k+ æ ç è n+1 2k+1 ö ÷ ø (1 + 1 n )n-2k ( u n )2k+1

= (n+1)!(1 + 1/n)n-2k (2k+1)!(n+1-2k)! æ ç è u n ö ÷ ø 2k   [(2k+1)(1 + 1 n ) +(n+1 - 2k)( u n ) ]  .

This will be nonnegative if and only if the quantity in square brackets is nonnegative. Since u > -1, this quantity exceeds

(2k+1)(1 + 1 n ) - (n + 1 - 2k)( 1 n ) = æ ç è n+1 n ö ÷ ø (2k + 1 - 1) - 2k n = 2k > 0 .

Thus, each consecutive pair of terms in the sequence

æ ç è n+1 2 ö ÷ ø (1 + 1 n )n-1( u n )2+ æ ç è n+1 3 ö ÷ ø (1 + 1 n )n-2( u n )3 + ¼

has a positive sum and so the desired result follows.