Subsections
``I think it's very important that people are encouraged to work on very
hard problems. The tendency today is to work on short and immediate
problems."
This is attributed to Andrew Wiles.
On Saturday, June 10th, 2000, Carl Pomerance gave a plenary lecture at the
Canadian Mathematical Society summer meeting at McMaster University,
Hamilton, Ontario, Canada. He listed his top 10 unsolved problems in
number theory.
015
I formulated the problems and so I am
accountable for any mistakes. The numbering of my list does not
necessarily agree with the numbering of Carl's list. -Ed.
- Goldbach Conjecture. In a letter to Euler in 1742, Goldbach
formulated the following conjecture.
Conjecture (Goldbach) Every even integer
A
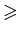 4 is
the sum of two primes.
4 is
the sum of two primes.
- Riemann Conjecture. For a complex number
s =
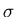 + it,
and
+ it,
and
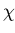 (n) a non-trivial Dirichlet character, let
and
Conjecture (Riemann Hypothesis-RH) All non-trivial zeros of
(n) a non-trivial Dirichlet character, let
and
Conjecture (Riemann Hypothesis-RH) All non-trivial zeros of
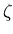 (s) lie on the line
(s) lie on the line
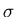 =
= 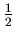 .
Conjecture (Extended Riemann Hypothesis-ERH)
All non-trivial zeros of L(s,
.
Conjecture (Extended Riemann Hypothesis-ERH)
All non-trivial zeros of L(s,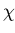 ) lie on the line
) lie on the line
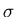 =
= 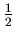 .
Let K be an algebraic number field,
.
Let K be an algebraic number field,
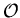 K its ring of
integers,
K its ring of
integers,
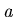 an ideal of
an ideal of
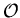 K, and
where the sum is over all ideals
K, and
where the sum is over all ideals
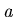 of
of
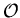 K, and
N
K, and
N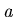 is the norm of
is the norm of
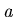 , defined to be the
index of
, defined to be the
index of
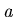 in
in
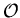 K.
Conjecture (Generalised Riemann Hypothesis-GRH)
All non-trivial zeros of
K.
Conjecture (Generalised Riemann Hypothesis-GRH)
All non-trivial zeros of
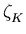 (s) lie on the line
(s) lie on the line
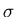 =
= 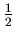 .
.
- Hardy-Littlewood Conjecture. For integers A
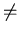 0, B,
and
C, let
0, B,
and
C, let
q(n) = An2 + Bn + C, for some n,
and
Q(
x) = #{
p 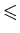 x
x :
p =
q(
n) for some
n }.
Conjecture (Hardy-Littlewood, 1923). There exists a constant
K > 0
such that
Q(
x)
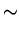 K
K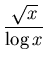
.
- Artin's Conjecture. Let A be a non-zero integer other
than
1, - 1, or a perfect square, and let NA(x) denote the number of primes
p
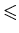 x for which A generates the cyclic group
x for which A generates the cyclic group
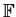 p* = { 1, 2, 3,..., p - 1 }.
Conjecture (Artin, 1927) There exists a constant K(A) > 0
such
that,
p* = { 1, 2, 3,..., p - 1 }.
Conjecture (Artin, 1927) There exists a constant K(A) > 0
such
that,
NA(
x)
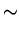 K
K(
A)
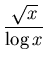
.
- ABC Conjecture. In 1980, Masser and Oesterlé
formulated the following conjecture.
Conjecture (Masser-Oesterlé, 1980) Let
n = p1
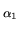 p2
p2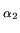 ... pk
... pk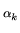 , and
rad (n)
, and
rad (n)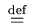 p1p2 ... pk. Suppose we have 3
integers A, B, C satisfying
(A, B) = (A, C) = (B, C) = 1, and A + B = C. Given
p1p2 ... pk. Suppose we have 3
integers A, B, C satisfying
(A, B) = (A, C) = (B, C) = 1, and A + B = C. Given
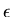 > 0, it is conjectured that there is a constant
K(
> 0, it is conjectured that there is a constant
K(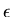 )
such that
)
such that
max(|
A|,|
B|,|
C|)
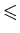 K
K(
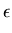
){
rad (
ABC)}
1 + 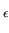
.
- Discrete Log Problem. Let G be a finite group with group
operation o,
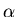
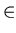 G,
H = {
G,
H = { 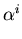 : i
: i 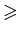 0 }
the subgroup generated by
0 }
the subgroup generated by 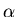 , and
, and
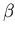
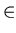 H.
Discrete Log ProblemFind the unique integer A such that
0
H.
Discrete Log ProblemFind the unique integer A such that
0 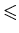 A
A 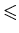 #H - 1 and
#H - 1 and
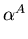 =
= 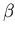 , where
, where 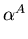 means
means
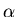 o
o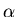 o ... o
o ... o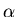 o
o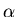 , A times.
, A times.
- Wieferich Primes. An odd prime p is called a Wieferich
prime
if p2 divides 2p - 1 - 1. The only known Wieferich primes are 1093
and 3511.
Wieferich Prime Problem Do there exist infinitely many primes
p such that p2 divides 2p - 1 - 1?
- Mersenne Primes. A Mersenne prime number is a prime of
the form 2p - 1. Notice every even perfect number; equal to the
sum of its proper divisors, is of the form
2p - 1(2p - 1);
6 = 2(22 - 1), 28 = 22(23 - 1), 496 = 24(25 - 1),...
Mersenne Prime Problem Do there exist infinitely many primes
p such that 2p - 1 is a prime? That is, do there exist infinitely
many even perfect numbers?
Conjecture (Wagstaff, 1983) There exists a constant K > 0
such that
#{
p 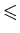 x
x : 2
p - 1 is prime }
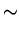 K
K loglog
x.
- Prime Gaps. Let pn denote the nth prime, and let
dn = pn + 1 - pn.
Prime Gap Problem For
pn + 1
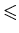 x, how big can
dn be?
x, how big can
dn be?
- Multiplication vs. Factoring. Modern cryptography is
based on our inability to factor large numbers fast.
Arithemetic Problem Prove or disprove the following
assertion which is at the base of the RSA cryposystem: It is harder
to factor a given number than to multiply given numbers together.
- On the Riemann Hypothesis.
Show that
for all n sufficiently large (
n
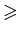 5041), where
5041), where 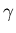 is
Euler's constant.
Theorem (Robin, G, 1984): This is equivalent to RH.
A. Ivic016 has shown
for
n
is
Euler's constant.
Theorem (Robin, G, 1984): This is equivalent to RH.
A. Ivic016 has shown
for
n 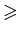 7,
7,
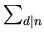
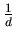 < 2.59 loglog n.
Let
where
< 2.59 loglog n.
Let
where
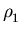 ,
,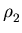 , ... is the list of all nontrivial zeros of
, ... is the list of all nontrivial zeros of
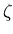 (s).
Theorem (Matijaševic, 1988): For all n, m,
(s).
Theorem (Matijaševic, 1988): For all n, m,
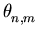 > 0
is
equivalent to
RH.
> 0
is
equivalent to
RH.
- On the Extended Riemann Hypothesis.
Theorem (Miller, G, 1975): ERH implies that primality
testing can be done in polynomial time P.
Is primality testing NP complete? If so, ERH implies P=NP.
- On the Generalized Riemann Hypothesis.
Theorem (Hooley, C, 1967): GRH implies Artin's conjecture.
- Hilbert's problem 8 (in 3 parts and concerned with RH, Goldbach's
conjecture and twin primes) is still unresolved since its announcement as
part of Hilbert's famous list of 23 problems. Notice that Hilbert's list
of 23 problems appears in the Bulletin (New Series) of the American
Mathematical Society (AMS) volume 37, #4, October 2000, pg. 407.
The Riemann Hypothesis has been supported by extensive numerical
calculations (the first 1.5 billion zeros satisfy RH) and various
heuristics, but such partial evidence is not convincing enough for all
mathematicians, including A.
Ivic. He points out
017 a
heuristic connected with moments of the zeta-functions: this would imply
the falsity of the Lindelöf hypothesis, and a fortiori that of the
Riemann
hypothesis! In the same paper he discusses other ``conditional disproofs"
of RH. Furthermore, in personal correspondence, he writes ``I don't think
there is much hope in working through Robin's equivalent."
The Clay Mathematics Institute (CMI) of Cambridge,
Massachusetts has named seven Millennium Prize Problems. The Scientific
Advisory Board of CMI selected these problems, focusing on important
classic questions that have resisted solution over the years. The Board
of Directors of CMI designated a 7 million prize fund for the solution to
these problems, with 1 million allocated to each. The problems were
announced on Wednesday, May 24, 2000, at the Collège de France. One
hundred years earlier, on August 8, 1900, David Hilbert delivered his
famous 23 open problems.
A mathematical description
(a leading specialist in the domain in
question has formulated each problem) as well as the rules for the CMI
millennium prize problems can be found via our website
(http://www.cms.math.ca/Students) by
following the links
In your area,
mathematics at UNBC,
news,
Clay Mathematics. The 7 problems are:
| P versus NP |
| The Hodge Conjecture |
| The Poincaré Conjecture |
| The Riemann Hypothesis |
| Yang-Mills Existence and Mass Gap |
| Navier-Stokes Existence and Smoothness |
| The Birch and Swinnerton-Dyer Conjecture |
Andrew J. Irwin
2001-03-19

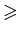 4 is
the sum of two primes.
4 is
the sum of two primes.
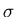 + it,
and
+ it,
and
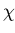 (n) a non-trivial Dirichlet character, let
and
(n) a non-trivial Dirichlet character, let
and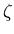 (s) =
(s) = 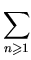
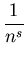 ,
L(s,Conjecture (Riemann Hypothesis-RH) All non-trivial zeros of
,
L(s,Conjecture (Riemann Hypothesis-RH) All non-trivial zeros of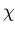 ) =
) = 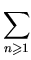
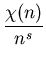 .
.
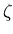 (s) lie on the line
(s) lie on the line
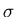 =
= 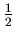 .
Conjecture (Extended Riemann Hypothesis-ERH)
All non-trivial zeros of L(s,
.
Conjecture (Extended Riemann Hypothesis-ERH)
All non-trivial zeros of L(s,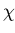 ) lie on the line
) lie on the line
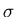 =
= 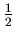 .
Let K be an algebraic number field,
.
Let K be an algebraic number field,
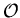 K its ring of
integers,
K its ring of
integers,
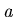 an ideal of
an ideal of
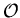 K, and
where the sum is over all ideals
K, and
where the sum is over all ideals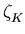 (s) =
(s) = 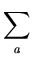
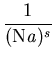 ,
,
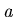 of
of
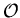 K, and
N
K, and
N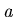 is the norm of
is the norm of
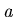 , defined to be the
index of
, defined to be the
index of
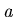 in
in
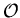 K.
Conjecture (Generalised Riemann Hypothesis-GRH)
All non-trivial zeros of
K.
Conjecture (Generalised Riemann Hypothesis-GRH)
All non-trivial zeros of
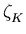 (s) lie on the line
(s) lie on the line
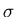 =
= 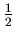 .
.
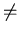 0, B,
and
C, let
q(n) = An2 + Bn + C, for some n,andQ(x) = #{ pConjecture (Hardy-Littlewood, 1923). There exists a constant K > 0 such that
0, B,
and
C, let
q(n) = An2 + Bn + C, for some n,andQ(x) = #{ pConjecture (Hardy-Littlewood, 1923). There exists a constant K > 0 such that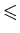 x : p = q(n) for some n }.
Q(x)
x : p = q(n) for some n }.
Q(x)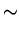 K
K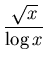 .
.
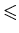 x for which A generates the cyclic group
x for which A generates the cyclic group
 p* = { 1, 2, 3,..., p - 1 }.
Conjecture (Artin, 1927) There exists a constant K(A) > 0
such
that,
NA(x)
p* = { 1, 2, 3,..., p - 1 }.
Conjecture (Artin, 1927) There exists a constant K(A) > 0
such
that,
NA(x)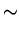 K(A)
K(A)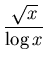 .
.
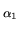 p2
p2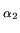 ... pk
... pk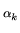 , and
rad (n)
, and
rad (n) p1p2 ... pk. Suppose we have 3
integers A, B, C satisfying
(A, B) = (A, C) = (B, C) = 1, and A + B = C. Given
p1p2 ... pk. Suppose we have 3
integers A, B, C satisfying
(A, B) = (A, C) = (B, C) = 1, and A + B = C. Given
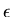 > 0, it is conjectured that there is a constant
K(
> 0, it is conjectured that there is a constant
K(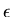 )
such that
max(| A|,| B|,| C|)
)
such that
max(| A|,| B|,| C|)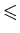 K(
K(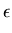 ){rad (ABC)}1 +
){rad (ABC)}1 + 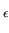 .
.
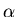
 G,
H = {
G,
H = { 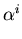 : i
: i 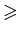 0 }
the subgroup generated by
0 }
the subgroup generated by 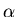 , and
, and
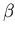
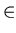 H.
Discrete Log ProblemFind the unique integer A such that
0
H.
Discrete Log ProblemFind the unique integer A such that
0 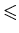 A
A 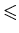 #H - 1 and
#H - 1 and
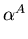 =
= 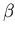 , where
, where 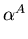 means
means
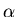 o
o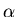 o ... o
o ... o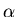 o
o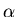 , A times.
, A times.
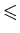 x : 2p - 1 is prime }
x : 2p - 1 is prime } 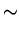 K loglog x.
K loglog x.
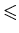 x, how big can
dn be?
x, how big can
dn be?
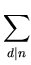
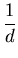 < e
< e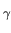 loglog n,
loglog n,
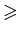 5041), where
5041), where 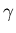 is
Euler's constant.
Theorem (Robin, G, 1984): This is equivalent to RH.
A. Ivic016 has shown
for
n
is
Euler's constant.
Theorem (Robin, G, 1984): This is equivalent to RH.
A. Ivic016 has shown
for
n 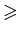 7,
7,
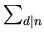
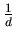 < 2.59 loglog n.
Let
where
< 2.59 loglog n.
Let
where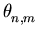 =
= 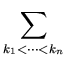
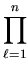 [
[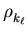 (1 -
(1 - 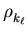 )]-m,
)]-m,
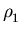 ,
,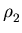 , ... is the list of all nontrivial zeros of
, ... is the list of all nontrivial zeros of
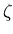 (s).
Theorem (Matijaševic, 1988): For all n, m,
(s).
Theorem (Matijaševic, 1988): For all n, m,
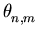 > 0
is
equivalent to
RH.
> 0
is
equivalent to
RH.
